Problem: Decide whether the following integral converges:
![]()
Solution:
In this integral there are two problems, namely each endpoint. Infinity is
obvious, and
![]()
We will now look at convergence of the two integrals, starting with the latter. Since this looks like a very simple integral, we will try to evaluate it:
![]()
(We already know that the last integral is divergent). This means that there is no need to investigate the second part (the integral from 1 to 2), the whole given integral is divergent.
Notes:
1. Note that the convergence of the integral we evaluated above cannot be
decided by our tests. First, try the comparison. For
![]()
Then also
![]()
and the Comparison test is inconclusive.
We could try to compare the given function to some powers that have
convergent integrals to infinity, but this is not possible. This should
become clear when we attempt limit comparison. The test function
![]()
If we try a higher power in the denominator, the function will be too small.
Precisely, for any
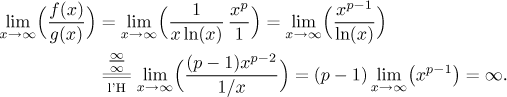
Thus powers do not help as test functions in the Limit Comparison test.
Now it is useful to recall the scale of powers at infinity. While
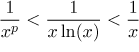 for large values of x. This explains why our tests could not work, the
given function manages to fall into the gap between convergent and
divergent test integrals. We could think of it as a refinement of our test
scale. In fact, one can show by evaluating as above that the integral
for large values of x. This explains why our tests could not work, the
given function manages to fall into the gap between convergent and
divergent test integrals. We could think of it as a refinement of our test
scale. In fact, one can show by evaluating as above that the integral
![]()
converges exactly if
2. Although it was not necessary to check on the integral from 1 to 2 to solve our problem, it is nevertheless a good exercise. Since we can easily integrate, we directly evaluate:
![]()
So this integral is also divergent. However, logarithm behaves quite
differently around 1 as compared to infinity. For instance, while around
infinity, logarithm cannot be compared to any power (as we saw above), for
values of x close to 1 we have
![]()
Justification now succeeds:
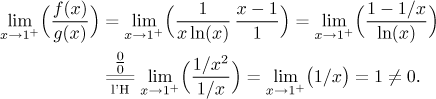
Since the test integral
![]()
diverges, by the Limit Comparison test, also the integral of f from 1 to 2 diverges.