Povrch rotačního tělesa

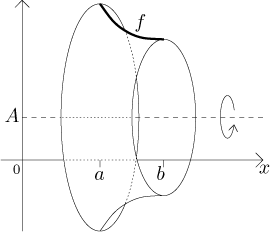
Uvažujme graf funkce f na intervalu ⟨a,b⟩.

Vodorovná osa rotace

Uvažujme povrch získaný rotováním tohoto grafu okolo osy rotace dané rovnicí y = A, kde A < min( f ).

Abychom našli jeho povrchový obsah, rozdělíme interval ⟨a,b⟩ na disjunktní podintervaly velikosti dx. Pro každý z nich uvažujme odpovídající kousek grafu funkce f. Protože takový podinterval je velice malý, můžeme předpokládat, že odpovídající kousek grafu f je kousek přímky o směrnici f ′(x). Můžeme tedy použít Pythagorovy věty k nalezení jeho délky, přesně jako jsme to udělali při výpočtu délky křivky.

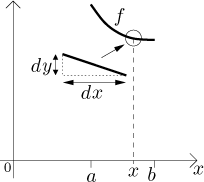
Když tento kousek grafu zrotujeme, obdržíme plášť komolého kužele. Abychom našli jeho obsah, vynásobíme délku tohoto kousku grafu vzdáleností, kterou urazil jeho střed během rotace, což je 2π krát poloměr, který je roven f (x) − A. Když to uděláme se všemi podintervaly intervalu ⟨a,b⟩, tak tím vlastně aproximujeme daný povrch plášti komolých kuželů:

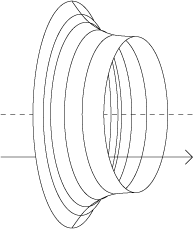
Sečtením jejich povrchových obsahů dostaneme

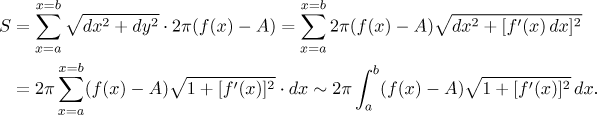
Jako obvykle použijeme k zajištění integrability toho nejjednoduššího, spojitosti:

Fakt.
Uvažujme povrch získaný rotací grafu funkce f na intervalu ⟨a,b⟩ okolo osy rotace dané y = A, kde A < min( f ). Jestliže má f spojitou derivaci na ⟨a,b⟩, pak je povrchový obsah tohoto povrchu roven

Uvažujme povrch získaný rotováním grafu funkce f okolo osy rotace dané rovnicí x = A, kde A < a.

Postupujeme zde vlastně stejně jako předtím. Rozdělíme graf na malé kousky odpovídající podintervalům délky dx na ose x. Jejich délky se spočítají stejně jako předtím, pak je zrotujeme. Jediný rozdíl je v tom, že teď je poloměr rotace roven x − A pro kousek grafu odpovídající podintervalu na pozici x.

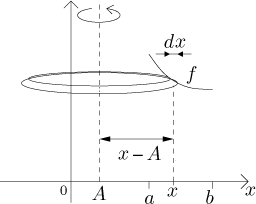
Pro povrchový obsah dostaneme

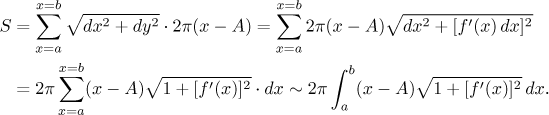
Máme tedy následující:

Fakt.
Uvažujme povrch získaný rotací grafu funkce f na intervalu ⟨a,b⟩ okolo osy rotace dané x = A, kde A < a. Jestliže má f spojitou derivaci na ⟨a,b⟩, pak je povrchový obsah tohoto povrchu roven

Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩. Předpokládejme, že y(t) ≥ 0 pro všechna t a že x(t) je rostoucí:

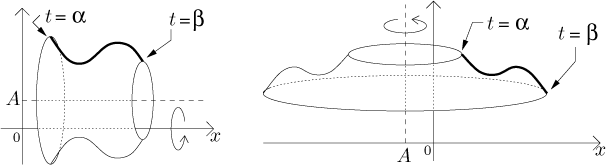
Teď budeme rotovat tuto křivku postupně kolem vodorovné a svislé osy a najdeme povrchový obsah. To ale bude snadné. Nejprve musíme najít délku malého kousku křivky, což uděláme z Pythagorovy věty úplně stejně, jako jsme to dělali při hledání délky křivky. Pak tento kousek rotujeme a obvod najdeme jako při předchozím výpočtu, jen musíme dosadit parametrické vyjádření. Dostaneme tedy následující:

Fakt.
Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩. Předpokládejme, že y(t) ≥ 0 pro všechna t a že x(t) je monotónní. Předpokládejme dále, že obě funkce mají spojitou první derivaci.

Povrchový obsah povrchu daného rotací této křivky okolo vodorovné osy rotace dané rovnicí y = A, kde A < min(y(t)), je roven

Povrchový obsah povrchu daného rotací této křivky okolo svislé osy rotace dané rovnicí x = A, kde A < min(x(t)), je roven

Hmotnost a těžiště
Zpět na Teorie - Aplikace