Obsah rovinného útvaru

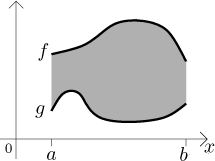
Víme, že určitý integrál dává matematický obsah oblasti mezi grafem integrované funkce a osou x. Z toho vyjdeme, když budeme chtít odvodit nějakou rozumnou formulku pro geometrický obsah. Nejprve zvolíme správný objekt: oblast mezi dvěma grafy na tomtéž intervalu.

Taková oblast je ideální. Předně je dostatečně obecná, a hlavně se s ní dá lehce pracovat. Všimněte si, že v našem obrázku jsou obě funkce kladné, takže jejich určité integrály dají geometrické obsahy oblastí pod jejich grafy. Obsah mezi grafy se pak dá jednoduše získat odečtením obsahu pod g od obsahu pod f:

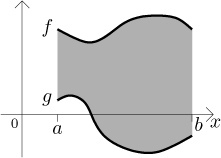
Tento vzorec se ukáže jako ten správný i pro obecnou pozici funkcí, jen si musíme dát pozor, abychom vždy identifikovali tu větší. Abychom viděli, proč by tato formulka mohla fungovat, podívejme se na příklad, kde funkce nezůstanou kladné:

Rozdělíme oblast mezi grafy na svislé pruhy šířky dx. Ze stejného důvodu, jako když jsme probírali význam určitého integrálu, můžeme předpokládat, že pruhy jsou tak tenké, že odpovídající kusy grafu jsou úsečky.

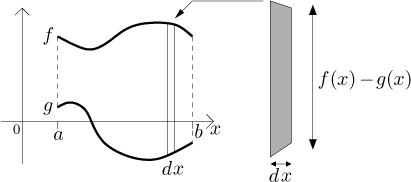
Obsah jednoho takového pruhu je roven šířce dx vynásobené výškou uprostřed, což je f (x) − g(x), zde využíváme znalosti, že f je ta větší funkce. Proto

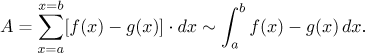
Každopádně máme následující:

Fakt.
Uvažujme oblast vymezenou shora grafem funkce f a zdola grafem funkce g na intervalu ⟨a,b⟩. Pokud jsou obě funkce Riemannovsky integrovatelné, obsah této oblasti je

Je možné uzavřít rozdíl funkcí do absolutní hodnoty, pak není třeba se starat o to, která je větší. Takový vzorec by byl obecnější a proto z matematického hlediska přijatelnější. My však víme, že absolutní hodnotu neumíme integrovat přímo a v konkrétních příkladech se jí zbavujeme rozdělením integrálu podle toho, kde je která funkce větší, takže jsme zase u našeho speciálního vzorce.

Poznámka: Rozdělení oblasti na vodorovné pruhy (velikosti dy) moc nepomůže:

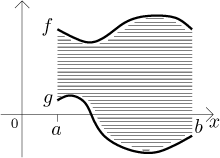
Jak vidíte z obrázku, dostaneme pruhy různých druhů. Některé začínají na úrovni x = a a jdou až na úroveň x = b, jiné začnou či skončí dříve, když dojdou ke grafu f nebo g. Poblíž spodního okraje máme dokonce situaci, kde dané úrovni y neodpovídá jen jeden vodorovný pruh, ale několik za sebou.

Znamená to, že nejde najít jeden společný vzorec pro délky pruhů, což zase znamená, že není šance vytvořit obecný vzorec pro sečtení jejich délek, tedy neexistuje vzorec pro obsah celé oblasti pomocí vodorovných pruhů. Popravdě řečeno, situace v tom obrázku je pořád ještě hodně pěkná. Obecně mohou grafy f a g hodně oscilovat nahoru a dolů a situace se pak stane nezvládnutelnou.

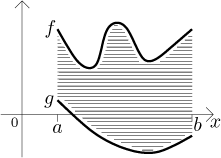
Evidentně je nemožné najít obsah takovéto oblasti pomocí vodorovných pruhů, zatímco svislé fungují skvěle.

Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩. Předpokládejme, že y(t) ≥ 0 pro všechna t a že x(t) je rostoucí:

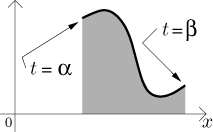
Můžeme předchozí trik s rozdělením aplikovat i na oblast pod touto křivkou. Jaký je obsah jednoho svislého pruhu? Výška (uprostřed) takového pruhu je dána jako y(t). Šířka je dána dx, ale proměnná x je transformací proměnné t, pro kteroužto situaci jsme viděli předpis v části Teorie - Integrace - substituce: dx = x′(t)dt. Dostaneme tedy

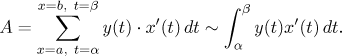
Je také možné použít parametrických rovnic k eliminaci parametru t pomocí inverzní funkce k funkci x a přejít do situace grafu funkce. Všimněte si, že používáme x pro dva rozdílné objekty: proměnnou a také funkci, která určuje, jak x záleží na t. Zatím jsme to zvládali, v následujícím výpočtu by se to ale příliš pletlo. Proto budeme na chvíli říkat této funkci h, tedy x = h(t). Teď už jsme připraveni identifikovat funkci f, která určuje stejnou křivku jako dané parametrické rovnice, pomocí eliminace parametru:

Můžeme tedy najít obsah pomocí nepřímé substituce:

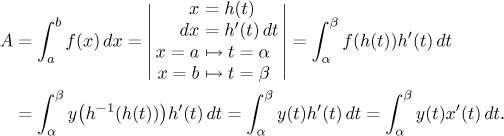
Pokud je x(t) klesající, křivka jde "zprava doleva" a derivace bude záporná. To se lehce spraví pomocí absolutní hodnoty. Pořád bychom měli nějak zajistit, že výsledný integrál existuje, tak zkusíme jako nejjednodušší řešení spojitost a dostaneme toto:

Fakt.
Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩. Jestliže y(t) ≥ 0 pro všechna t, x(t) je monotónní a funkce x′ a y jsou spojité, pak obsah oblasti pod touto křivkou je

Uvažujme křivku v polárních souřadnicích danou předpisem ϱ = ϱ(φ) pro φ z ⟨α,β⟩. Předpokládejme, že ϱ(φ) ≥ 0 pro všechna φ.

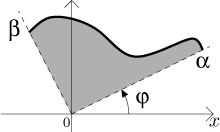
Tentokráte uvažujeme oblast jiného tvaru, takže není možné převést situaci do předchozího rámce. Musíme to zkusit jinak. Použijeme zde fakt, že proměnná φ má přesný význam - je to úhel. Můžeme tedy rozdělit úhel ⟨α,β⟩ na malé podúhly velikosti dφ, čímž obdržíme spoustu "vějířků". Protože jsou tak tenké, můžeme předpokládat, že jejich vnější okraj není nějaká křivka, ale kousek kružnice se středem v počátku.

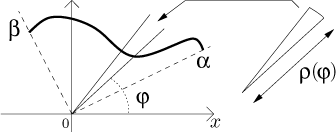
Víme, že obsah takového vějířku je dán jako polovina úhlu ve vrcholu v radiánech krát druhá mocnina poloměru. Sečtením získáme

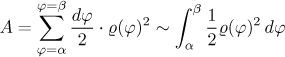
Musíme také zabezpečit, že se křivka nezavine kolem počátku víc než jednou, protože pak by se oblast překrývala a některé části by byly započítány vícekrát.

Fakt.
Uvažujme křivku v polárních souřadnicích danou předpisem ϱ = ϱ(φ) pro φ z ⟨α,β⟩, kde β − α ≤ 2π. Předpokládejme, že funkce ϱ(φ) je spojitá a že ϱ(φ) ≥ 0 pro všechna φ. Obsah šrafované oblasti pak je

Délka křivky
Zpět na Teorie - Aplikace