Hmotnost a těžiště

Úsečka

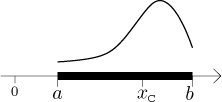
Uvažujme úsečku ⟨a,b⟩ na ose x, jejíž hustota je dána funkcí ϱ(x).

Rozdělíme ji na malé kousky velikosti dx.

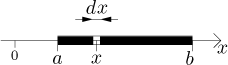
Můžeme předpokládat, že na kousku na pozici x se hustota díky jeho malému rozměru nemění a je rovna ϱ(x), takže hmotnost takového kousku je ϱ(x) krát dx. Sečtením hmotností všech kousků dostaneme vzorec pro hmotnost úsečky:

Těžiště leží na ose x. Abychom našli jeho x-ovou souřadnici, nejprve si představíme, že úsečka rotuje kolem osy y, a vypočítáme její statický moment M_y. Víme, jak to udělat pro bodovou hmotu: M je rovno poloměru rotace krát hmotnost. Pokud tedy rozdělíme úsečku na malé kousky velikosti dx, můžeme takto spočítat statický moment každého kousku: M = xϱ(x)dx. Sečtením dostaneme celkový moment:

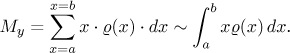
Souřadnice x_c těžiště splňuje rovnici M_y = mx_c. Tu je lehké vyřešit:

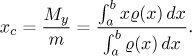
Uvažujme graf funkce f na intervalu ⟨a,b⟩. Předpokládejme, že hustota v bodech této křivky je dána funkcí ϱ(x).

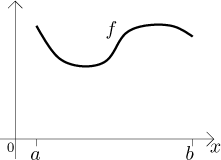
Rozdělíme interval ⟨a,b⟩ na malé kousky velikosti dx. Kousku na pozici x odpovídá kousek grafu funkce f. Protože je tento kousek grafu tak malý, můžeme předpokládat, že je to kousek přímky, a přesně jako při výpočtu délky křivky najdeme pomocí Pythagorovy věty velikost tohoto kousky grafu. Protože díky jeho malé velikosti múžeme rovněž předpokládat, že se hustota nestačí změnit a je rovna ϱ(x), dostaneme vynásobením hustoty s délkou hmotnost tohoto malého kousku. Celková hmotnost křivky se pak dostane, když hmotnosti kousků sečteme integrací:

Abychom našli souřadnice těžiště, budeme muset najít statické momenty vzhledem k obou osám. Rozdělíme graf na malé kousíčky jako předtím a najdeme hmotnost kousku odpovídajícímu pozici x. Statický moment tohoto kousku vzhledem k ose y se spočítá jako jeho hmotnost krát jeho vzdálenost od osy y, což je x. Statický moment tohoto kousku vzhledem k ose x se spočítá jako jeho hmotnost krát jeho vzdálenost od osy x, což je f (x).

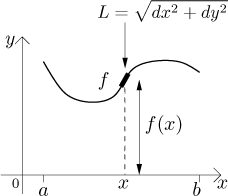
Když tyto momenty sečteme integrací, dostaneme momenty celé křivky. Vydělením hmotností křivky pak dostaneme souřadnice těžiště, protože ty zase musí splňovat rovnici jako u úsečky:

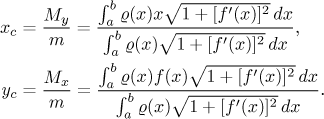
Uvažujme rovinnou oblast vymezenou shora grafem funkce f a zdola grafem funkce g na intervalu ⟨a,b⟩. Předpokládejme, že hustota v bodech této oblasti záleží pouze na x a je rovna ϱ(x).

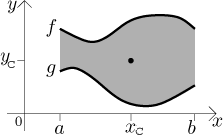
Rozdělíme tuto oblast na svislé proužky šířky dx. Můžeme předpokládat, že na každém proužku je hustota konstantní, takže jeho hmotnost je rovna hustotě krát obsah proužku, což je jeho šířka dx krát výška uprostřed.

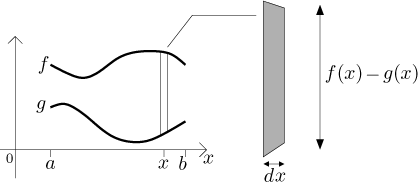
Sečtením hmotností všech proužků získáme celkovou hmotnost oblasti:

Abychom našli souřadnice těžiště, budeme zase muset najít statické momenty vzhledem k obou osám. Nejprve spočítáme moment vzhledem k ose y.

Protože na každém proužku předpokládáme konstantní hustotu ϱ(x) a všechny body takového proužku jsou stejně daleko od osy rotace, statický moment celého proužku je dán jeho hmotností ϱ(x)[f (x) − g(x)]dx vynásobenou statickým momentem jednoho bodu jako u úsečky. Sečtením momentů všech proužků dostaneme

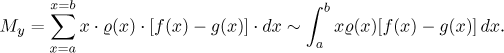
Teď zkusíme najít statický moment vzhledem k ose x. To nebude tak snadné, protože když budeme uvažovat jeden takový proužek jako předtím, jeho body mají rozdílné vzdálenosti od osy rotace, tj. od osy x. Všimněte si, že vůbec nepomůže rozložení oblasti na vodorovné pruhy. To, že se v bodech takového pruhu mění hustota, je samo o sobě nepříjemné, ale ještě horší je, že bychom dostali pruhy různých typů. Některé sahají od úrovně a po b, jiné jen od a po graf f atd., obecně to může být ještě divočejší.

Takže jsme zase zpátky u svislých pruhů. Podíváme se na statický moment jednoho takového pruhu jako na samostatný problém. Vlastně je to docela lehké, všimněte si, že rotujeme úsečku [f (x),g(x)] kolem vodorovné osy, takže pokud prohodíme osy, dostaneme stejný obrázek jako na začátku:

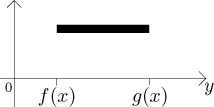
Moment rotace tedy dostaneme úplně stejně jako u úsečky, jen si musíme dát pozor, že používáme proměnnou y a že hustota je konstantní:

Toto byl moment jedné úsečky, když jej vynásobíme dx, dostaneme statický moment pruhu. Sečtením momentů všech pruhů dostaneme statický moment celé oblasti vzhledem k ose x:

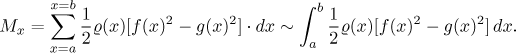
Souřadnice težiště najdeme pomocí momentů vzhledem k osám stejně jako u křivky, takže

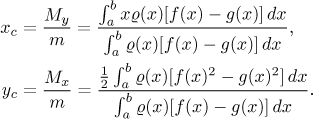
Uvažujme rovinnou oblast vymezenou shora grafem funkce f a zdola grafem funkce g na intervalu ⟨a,b⟩. Předpokládejme, že hustota v bodech této oblasti záleží jen na souřadnici x a je rovna ϱ(x). Tuto oblast zrotujeme kolem osy x a dostaneme těleso:

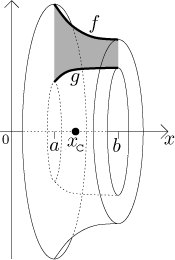
Abychom našli jeho hmotnost, uvažujme v oblasti svislé proužky o šířce dx. Po rotaci takového proužku dostaneme disk s otvorem ve středu. Všimněte si, že můžeme předpokládat, že jeho hustota je všude konstantní, protože je tak tenký, že se hustota nemůže příliš změnit (záleží jen na x). Jeho hmotnost je tedy rovna hustotě krát objem, který spočítáme úplně stejně, jako když jsme počítali objem rotačních těles metodou disků. Sečtením získáme celkovou hmotnost:

Těžiště leží na ose x. K získání jeho x-ové souřadnice potřebujeme najít moment vzhledem k rovině yz. K tomu zase použijeme ty disky. Všimněte si, že pro jeden určitý disk, všechny jeho body mají stejnou hmotnost (neboť mají stejnou hustotu) a také stejnou vzdálenost od roviny yz. Moment disku lze tedy spočítat jako tato vzdálenost x krát hmotnost disku. Sečtením dostaneme

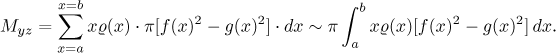
Jako předtím spočítáme x-ovou souřadnici těžiště z rovnice M_yz = mx_c. Dostaneme

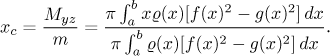
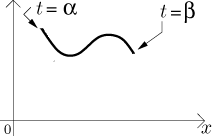
Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩. Předpokládejme, že y(t) ≥ 0 pro všechna t a že x(t) je rostoucí:

Pro zjednodušení budeme uvažovat homogenní útvary. Jejich hmotnost je pak dána jako délka/obsah/objem (viz příslušné sekce) násobený danou konstantní hustotou. Teď se podíváme na těžiště, v jehož vzorcích se hustota vykrátí.

Výpočty jsou vlastně stejné, jako tomu bylo předtím, příslušný útvar je rozložen na kousky a počítají se statické momenty. Jediný rozdíl je v tom, že se musí použít parametrických rovnic, ale příslušné postupy již byly odvozeny v kapitolách o obsahu a délce křivky. Dostaneme tak následující:

Fakt.
Uvažujme parametrickou křivku x = x(t), y = y(t) pro t z ⟨α,β⟩. Předpokládejme, že y(t) ≥ 0 pro všechna t a že x(t) je rostoucí. Předpokládejme dále, že x a y mají spojitou první derivaci.

Těžiště křivky samotné má souřadnice

Těžiště oblasti pod touto křivkou má souřadnice

Těžiště povrchu získaného rotací této křivky kolem osy x leží na ose x a jeho x-ová souřadnice je

Těžiště tělesa získaného rotací oblasti pod křivkou kolem osy x leží na ose x a jeho x-ová souřadnice je

Všimněte si, že jsme v posledních dvou zlomcích zkrátili 2π v předposledním a π v posledním. To znamená, že pokud byste potřebovali samotné momenty, musíte vzorce z těchto čitatelů vynásobit odpovídajícím faktorem (a ve všech parametrických vzorcích také hustotou).

Derivace integrálu
Zpět na Teorie - Aplikace