Příklad: Najděte obsah oblasti

Řešení: Nejprve musíme identifikovat oblast. Potřebujeme zjistit, pro která x má nerovnost smysl, to jest pro která x je funkce x + 4 větší než nebo rovna x² − x + 1. Tyto dvě funkce se protínají v bodech x = −1 a x = 3, máme tedy následující obrázek:

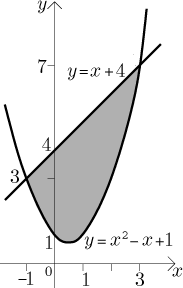
Oblast má ten správný tvar, takže můžeme přímo integrovat, dáme si pozor, abychom správně napsali větší funkci mínus menší funkci:

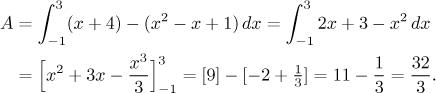
Teď to zkusíme jinak, prohodíme osy. Nejprve musíme najít inverzní funkce. Všimněte si, že není možné najít inverzní funkci k té kvadratické funkci, protože ta není prostá na ⟨−1,3⟩. Musíme tedy pro ni uvažovat dvě inverzní funkce:

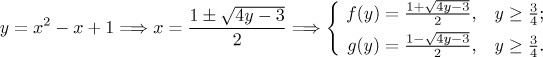
Dostaneme tedy

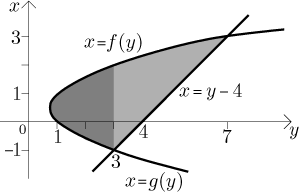
Teď vidíme, že oblast není základního typu, protože její dolní okraj není definován jednou, ale dvěma funkcemi. Abychom nalezli obsah, musíme oblast rozdělit na dvě části, jak je znázorněno v obrázku. Tak dostaneme

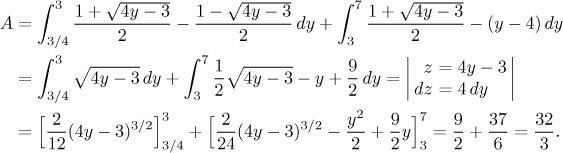
Poznámka:
Pokusíme se zde vysvětlit, jak se dají sestavit správné integrály, aniž by si člověk musel pamatovat vzorce. Nejprve zkusíme svislé řezy.

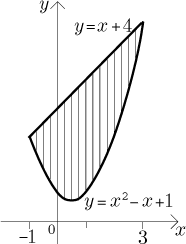
Celkový obsah dostaneme sečtením obsahů všech pruhů, neboli sečtením jejich délek vynásobených šířkou dx. Protože každý pruh je určen volbou proměnné x, sečteme je změnami x, tj. integrací vzhledem k dx. Délka pruhu je rovna y-ové souřadnici jeho horní hrany mínus y-ová souřadnice dolní hrany, ale protože integrujeme s dx, musí být tato informace dodána v jazyce x. Naštěstí pro nás máme přávě tuto informaci v obrázku. Dostaneme tedy

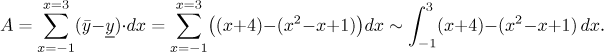
Teď zkusíme vodorovné pruhy.

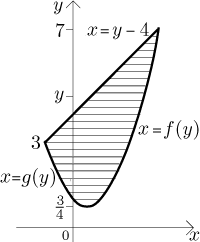
Zase dostaneme celkový obsah sečtením obsahů všech pruhů. Teď je jejich šířka dy, rovněž pozice určitého pruhu je dána volbou hodnoty proměnné y, což naznačuje, že pruhy sečteme měněním proměnné y; z obrázku se zdá, že bychom měli jít od 3/4 do 7. Sčítat znamená integrovat, takže budeme integrovat vzhledem k y. To vypadá přirozeně, protože měníme pruhy změnami y a v úvahách se už objevil diferenciál dy.

Pro určitý pruh (odpovídající určité zvolené hodnotě proměnné y) najdeme jeho délku jako rozdíl x-ová souřadnice horního (pravého) konce mínus x-ová souřadnico dolního (levého) konce, a protože integrujeme s dy, musíme tuto informaci dát v jazyce y. Konce pruhů leží na zadaných křivkách a my potřebujeme upravit tuto informaci do tvaru x rovná se nějakému výrazu s y. To znamená, že od daných funkcí musíme přejít k inverzním. Protože ale levé konce pruhů nejsou všechny na jedné křivce, musíme uvažovat dva typy pruhů, což vede ke dvěma integrálům. Nakonec tak dostaneme

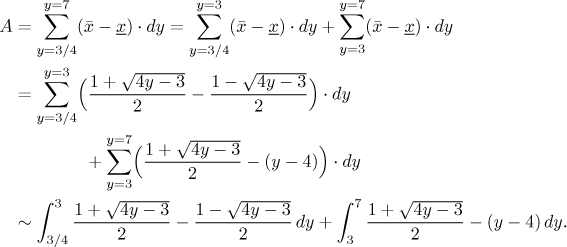
Použili jsme tento příklad, abychom ukázali, jak se rozhodnout, zda použít svislé řezy (integrace s dx) nebo vodorovné řezy (prohození os, integrace s dy). Vždy se snažíme použít ten způsob, který vede k hezčím funkcím k integrování, a pokud možno volíme tu variantu, která zahrnuje méně typů pruhů. Nejlepší případ je ten, kdy existují pruhy jen jednoho typu, což znamená, že obsah oblasti lze spočítat jedním integrálem.

Další příklad
Zpět na Řešené příklady - Aplikace