Problem: Determine whether the following series converges.
![]()
Solution: The given series is a sum of two series. We will look at each of them separately and hope that the two results can be put together.
First consider the series
![]()
This is a series that can be converted to a geometric series.
![]()
Since
Now we will look at the series
![]()
When we see factorial, we immediately think of the Ratio test.
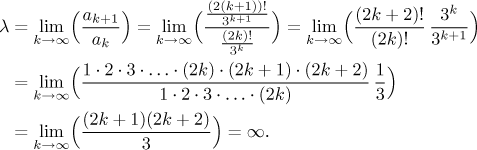
Since
Since the given series is the sum of a convergent and a divergent series, it is divergent.
Are there any alternatives? Concerning the second series, there is only one other reasonable way and it is perhaps even easier than the above approach. We know that factorial beats exponentials, therefore obviously the terms ak go to infinity, in particular they do not go to zero and so the corresponding series diverges by the necessary condition.
Other tests do not help here. Because of the factorial, we cannot hope to integrate and so the Integral test is out, it also makes using the Root test problematic. Finally, since there are no parts to ignore, we cannot hope to use comparison tests.
Determining convergence of the first series was very simple, but out of curiosity, is there any alternative? Again, this series is so simple that we cannot hope to simplify it and do comparison, but other tests work fine.
Since the function
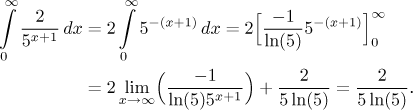
Since this improper integral converges, also the appropriate series converges.
Also the Root test works.
![]()
Since
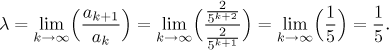
So also this confirms convergence (as expected, the constants in the Root test and the Ratio test are always the same).