Problem: Determine whether the following series converges.
![]()
Solution: The terms of this series are positive, so we may use all
the nice tests, but perhaps we should start by looking closer at these
terms. We see that
For series featuring powers we often use the Ratio test. How does the relevant ratio look like?
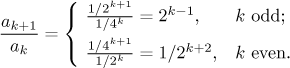
When k grows to infinity, then the odd ratios run away to infinity,
while the even ones go to zero. This shows that the limit for
λ
does not exist and the Ratio test does not work in its limit version.
The dual behavior shows that even the more general versions of Ratio test
(those with inequalities) do not work, since we cannot force the ratio
How about the Root test?
![]()
Just like with the Ratio test, the limit for
ϱ does not exist and so the limit version of the Root test does not
work. However, here we have a chance to use the more general version with
inequalities. Indeed, if we take
![]()
This proves that the given series is convergent.
Alternative: We could also try to use comparison. Due to the schizophrenic nature of this series we cannot hope to say that the terms look like a certain something for k large, which rules out the Limit comparison test, but we actually have a nice opportunity to use the plain Comparison test. We have
![]()
Since the series on the right converges
(it is a geometric series
with
Alternative: There is yet another interesting trick that one could
try. The given series has terms of two kinds, thus we can try to separate
them into two independent series. We therefore express it as the sum of the
series
![]()
What can we say about convergence of these two series? At the first glance we did not really improve our situation, both of them are of dual nature again, but - and that is the trick - zeros can be dropped from a series without any trouble. Thus we can rewrite these series using the usual expressions for even and odd numbers as follows.
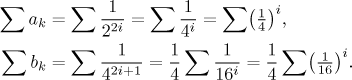
We see that in both cases we have
geometric series, both have