Problem: Determine whether the following series converges.

Solution: The terms of this series are positive, so all the nice tests can be used, and they obviously converge to zero as a sequence, which means that there is a chance for convergence. Note that the behavior of this series depends on the parameter p, so it can be expected that the answer will also depend on p.

What tests can we use? Since the terms of this series feature only k and logarithm, experience suggests that this is not a good idea to use the Root test or the Ratio test. Indeed,

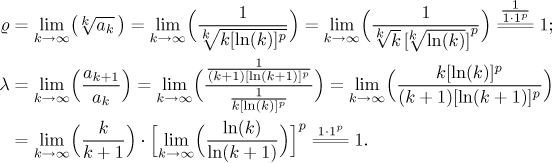
In both cases we obtained the indecisive value 1. By the way, in the limits above we used the following calculations to work out the indeterminate power and indeterminate ratio:

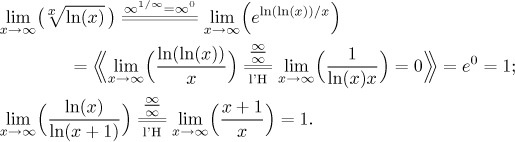
We often get good help from comparison. Here we can try to get rid of the logarithm. Since dropping it will substantially change the nature of the terms, we cannot use the Limit comparison test (where we say that a_k is essentially just like b_k), but we can hope for the plain Comparison to work. However, note that when we start ignoring the logarithmic part, the new expression may be both larger or smaller - depending on the value of p.

First, if p is negative or zero, then we have

We know that the series on the right diverges because it is the famous harmonic series, or we use the p-test. The given series is still larger, so by comparison it also must be divergent. Thus we know what happens for p at most zero. What about p positive? Then we have

Now comparison goes the wrong way and we cannot say anything. Is there a way to get some estimate from below? Actually, there is, since we know that powers beat logarithms. This means that for large k we can majorize the logarithmic part by a power of arbitrary positive exponent c:

Since we do not want to loose too much in this comparison, we can try to take c very small (the inequality is then true only for really large k, but that's enough), but no matter how little c we take, we are already loosing too much in that comparison. Indeed, the p-test stipulates that the series on the right converges for any 1 + c > 1, so we have a convergent series on the right and the comparison is useless, the inequality goes the wrong way. We see that comparison does not help for p positive.

Thus we at last turn to the test that is less popular but here it is the obvious choice, namely the Integral test. The function f (x) = 1/(x[ln(x)]^p) is positive and decreasing for large x, therefore we can pass to integral.

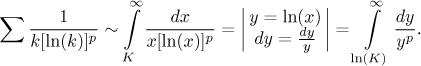
The p-test now tells us that the integral converges exactly if p > 1 and the same is then true for the series.

Conclusion: The given series converges if and only if p > 1.

Of course, an experienced series solver would go to the Integral test right away, but then you would miss all the suspense and the neat way in which comparison proved divergence for p negative or zero.

Is there an alternative? In fact there is, in the section More tests in Theory - Testing convergence you find some condensation tests that can help here. We commented on positivity and decrease of terms above, so the technical assumptions of the Cauchy test are satisfied. This allows us to pass to investigating the series

Now we apply the p-test and get the same answer, namely this series and therefore also the given series converge exactly if p > 1.

We can also apply the Ermakoff test.

We see that if p < 1, then r = ∞ and thus the given series diverges. If p > 1, then using l'Hôpital's rule (or the rule "powers beat logarithms") we get that r = 0 and the given series converges. Note that this test is inconclusive if p = 1.

Next problem
Back to Solved Problems - Testing convergence