Problem: Determine whether the following series converge.
![]()
Solution: We start with the first series. Its form invites us to use the Root test.
![]()
Since
Now we pass to the second given series. Is the Root test so nice again? This time we get an indeterminate power and we have to use the appropriate trick, see Sequences - Methods Survey - Limit.
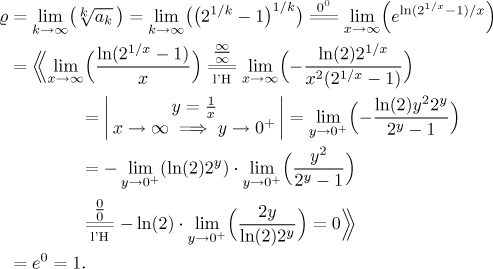
So in this case the Root test does not help, obviously the Ratio test would
be also inconclusive and so we have to look elsewhere for help. While the
function
How is it with comparison tests? We could try the obvious comparison
![]()
but since the large series on the right diverges (its terms do not go to 0),
it is useless. What else can we do? Evaluating ratio of successive terms
looks like a very bad business, so it is not a good idea to try even more
complicated refinements of the Ratio test (like Raabe test etc.). We may try
another angle: What do we know of ak when k
is large? Then
![]()
so we may guess that for large values of k we have
![]()
If we want to use the Limit comparison test, we have to justify such a claim.
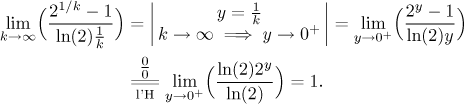
Now we are justified to compare
![]()
Since the test series on the right diverges (it is the famous harmonic series, or see the p-test), it follows that also the given series diverges.