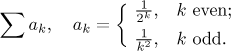
Problem: Investigate convergence of the following series. (Does it converge? If it does, then how?)

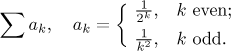
Solution: Note that all the terms are positive, so convergence and absolute convergence are the same for it. Thus it is remains to check on convergence and we have all the nice tests for series with positive terms available.

Since the terms of the series consist of powers, the natural candidate would be the Ratio test. Due to the dual nature of terms we will explore what the relevant ratios are doing separately for even and odd k's. Using l'Hôpital's rule we get

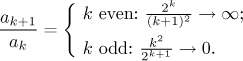
We see that the sequence {a_k+1/a_k} consists of two subsequences, one going to infinity and one to zero. Thus the whole sequence cannot be convergent and we have no λ. Do we get any help from the more general versions of the Ratio test (see Root and Ratio test in Theory - Testing convergence)? Given the two subsequences above (even and odd terms) we immediately get that limes superior is infinity, so this does not help. How about the general version with inequalities? Since one subsequences goes to a number less than 1 and the other to a number greater than 1, we cannot force the whole sequence to either stay above 1 or stay sharply below 1. There are no more versions, the Ratio test fails us completely.

How about the Root test? Again, we first look at what the even and odd terms are doing.

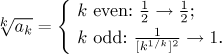
So again we have no limit. This time we have a finite limes superior, but it is equal to 1 and thus it does not help. How about the general version with inequalities? Note that all terms (a_k)^1/k are less than one, so the general Root test cannot give divergence, but they (or at least some of them) also approach 1 arbitrarily close, so we are unable to use the convergence part of that statement either. Therefore also the Root test did not help.

What other test could help? Since the terms are not given by one formula, the Integral test is clearly out. Our only hope now lies in some comparison. The results above suggest that there is no limit comparison possible, since the even and the odd terms behave in entirely different ways; the scale of powers shows that the even terms go to zero incomparably faster than the odd terms.

Thus the only hope remains with comparison. Actually, the last sentence of the above paragraph suggests one possible approach. It is relatively simple to check that 2^k is greater than k² for k at least 5 (or we just appeal to the above-mentioned scale of powers and conclude that such inequality must be true for large k), therefore we get comparison

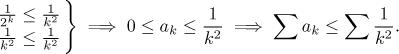
Since the series on the right converges (see the p-test or the Example there, this series is quite well-known), it follows that also the given series converges, therefore also converges absolutely.

Alternative: There is another interesting trick that one could try. The given series has terms of two kinds, thus we can try to separate them into two independent series. We therefore express it as the sum of the series  ∑ b_k  and  ∑ c_k,  where

What can we say about convergence of these two series? At the first glance we did not really improve our situation, both of them are of dual nature again, but - and that is the trick - zeros can be dropped from a series without any trouble. Thus we can rewrite these series using the usual expressions for even and odd numbers as follows.

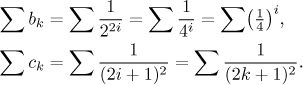
We see that the first series is a geometric series with |q| < 1, therefore it converges. We rewrote the second series to feature the traditional index k, it was not necessary but it is good to help ourselves a bit, we are used to this index. We see right away that also this second series is convergent, we prove it for instance by the following comparison it with a series that we already saw above.

The sum of two convergent series again converges, which confirms the convergence of the given series.

Next problem
Back to Solved Problems - Testing convergence