Basické systémy funkcí

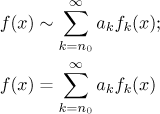
Začneme jedním zajímavým výsledkem. Nejprve jej uvedeme v klasickém hávu.

Věta (Stone-Weierstrassova věta).
Nechť f je funkce na omezeném uzavřeném intervalu I. Jestliže je spojitá, pak pro každé ε > 0 existuje polynom P takový, že | f (x) − P(x)| < ε pro všechna x z M.

To znamená, že každou spojitou funkci lze aproximovat pomocí polynomů libovolně dobře na omezených uzavřených intervalech. Teď to řekneme jiným jazykem.

Pro každou funkci f, která je spojitá na omezeném uzavřeném intervalu M, existuje posloupnost polynomů {P_n} taková, že P_n ⇉  f na M.

Tato věta je rozhodně užitečná, ale má jednu nevýhodu. Když chceme lepší a lepší aproximaci, tak obvykle potřebujeme vyšší stupně u P_n. Ona věta ovšem nezaručuje, že "delší" polynomy budou mít něco společného s "kratšími", jak je tomu u Taylorova polynomu při použití stejného středu a, když jen měníme stupeň. Z tohoto pohledu není ona věta výše postačující a my použijeme Taylorovy polynomy jako inspiraci pro následující rozpravu.

Stone-Weierstrassovské aproximace a Taylorovy polynomy nás zajímají z jednoduchého důvodu. Rádi bychom nahradili danou funkci, která se nám třeba moc nelíbí, nějakou hezčí funkcí, aniž bychom mnoho ztratili. Co znamená to "hezčí funkce"? Obvykle začneme s množinou nějakých pěkných a jednoduchých funkcí, to je základ pro naši práci, a "hezčí funkcí" míníme všechny funkce, které lze získat jako lineární kombinace oné základní množiny. Například když aproximujeme pomocí polynomů, tak je základním systémem množina všech mocnin x^k, jejich lineární kombinace jsou právě polynomy. Teď to dáme na papír přesně.

Je dána množina M (pro jednoduchost budeme předpokládat, že je to interval), uvažujme množinu V všech funkcí definovaných na M. Potom je V lineární prostor. Budeme uvažovat posloupnost funkcí { f_k} z V, která tvoří lineárně nezávislou množinu. To bude náš zvolený basický systém a jeho nezávislost znamená, že není zbytečně velký, všechny jeho funkce přispívají. První krok je uvažovat lineární podprostor, který tyto funkce generují. Pokud například vezmeme populární příklad f_k(x) = x^k, tak lineární podprostor, který tento systém generuje, je přesně prostor všech polynomů. Už jsme viděli, že tento prostor je dostatečně velký na to, aby aproximoval libovolně blízko všechny spojité funkce na M v případě, že M je omezená a uzavřená.

To nás přivádí k tomu hlavnímu. Jak už jsme poznamenali, dáváme přednost situaci, kdy zlepšovaní kvality aproximace znamená přidávat členy k již existující aproximaci. To znamená, že když máme basický systém { f_k}, tak nás zajímá prostor všech "nekonečných lineárních kombinací", tedy prostor všech konvergentních řad ve tvaru  ∑ a_kf_k. Rádi bychom identifikovali či nějak popsali tento prostor. To obvykle znamená odpovědět na několik zásadních otázek.

Jaké jsou ony důležité otázky? Je-li dána lineárně nezávislá množina funkcí { f_k}, tak chceme znát následující:
 •  Které funkce f lze obdržet jako součet řady  ∑ a_k f_k?
 •  Jestliže f = ∑ a_k f_k, jak najdeme příslušné koeficienty a_k?
 •  Jestliže f = ∑ a_k f_k, je ta konvergence stejnoměrná? Je absolutní?

V konkrétních případech bývá obvykle velice obtížné tyto otázky zodpovědět, a to i pro pěkné systémy. Často postupujeme následovně:

• Většinou jsme schopni určit nějaký rozumný prostor funkcí, pro které můžeme zaručit, že půjdou vyjádřit jako  ∑ a_k f_k. Většinou také víme, že jsou i další funkce, pro které se to dá udělat, takže vlastně tu první otázku výše velice zřídka umíme zodpovědět, mimo jiné proto, že jakmile opustíme onen rozumný prostor, tak se věci rychle komplikují a bývá to škaredé. Proto se (alespoň z praktického pohledu) obvykle rádi spokojíme s prostorem, který možná neodpovídá na naši otázku, ale je pěkný a věci tam fungují.
• Obvykle také umíme dokázat, že když máme f = ∑ a_k f_k, pak a_k musí být nutně dány určitým konkrétním vzorcem. Takový výsledek je zajímavý ze dvou důvodů. Za prvé, dává nám jednoznačnost vyjádření ve formě řady, což je zajímavé teoreticky. Za druhé, říká nám to, že když chceme vyjádřit nějakou funkci jako řadu, tak koeficienty dané oněmi vzorci jsou jedinými kandidáty, protože jiné prostě nemůžou fungovat.
• Pak je tady ještě zásadní otázka. Je nám dána rozumná funkce f (z onoho rozumného prostoru diskutovaného v prvním bodě) a pro ni najdeme koeficienty a_k podle vzorců s předchozího bodu; konverguje pak výsledná řada  ∑ a_k f_k  opravdu k f?
  Všimněte si, že to neplatí automaticky, protože implikace v předchozím bodě jde v opačném směru, a odpověď je překvapivě často záporná.
  

Při práci se systémy funkcí proto často vidíme následující značení.

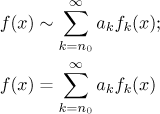
První řádek znamená, že jsme vzali f a vytvořili koeficienty a_k podle speciálních vzorců, které jsme našli v oné "špatné implikaci". Toto značení proto nezaručuje, že součet vzniklé řady je opravdu roven funkci f, ze které vzešla.
Druhý řádek znamená, že f je rovna součtu jisté řady. Všimněte si, že pokud jsme nedokázali výsledek o jednoznačnosti, pak tato řada nemusela nutně vzejít z oněch zvláštních vzorců.

V následujících sekcích prozkoumáme dva užitečné basické systémy funkcí. Nejprve se podíváme na systém daný mocninami x^k (mocninné řady a Taylorovy řady). Tento systém používáme k aproximování "pěkných" funkcí a je to asi nejznámější systém. Druhý systém (Fourierovy řady) je založen na funkcích sin(kt) a cos(kt), dost dobře mu jde kódování funkcí, které nejsou zrovna "pěkné" (funkce s nespojitostmi) a má mnoho aplikací při zpracování signálů, kódování a podobně.

Mocninné řady
Zpět na Teorie - Řady funkcí