Věta.
Nechť
Nechť c je libovolné reálné číslo, nechť f a g jsou
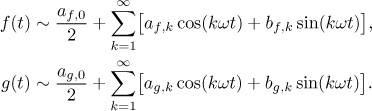
Pak
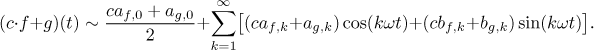
Zde se podíváme na vlastnosti, které obvykle očekáváme od rozvoje v řadu (jak se chová vzhledem k obvyklým operacím a jak reaguje na transformace funkcí). Pak se podíváme na alternativní způsoby zápisu Fourierových řad, jmenovitě amplitudově-fázový tvar a komplexní tvar.
Začneme s výsledkem, který není zcela relevantní k hlavnímu tématu této sekce, ale je někdy užitečný, tak se na to rychle podíváme.
Věta.
NechťT > 0, označmeω = 2π/T.
Pro libovolnouT-periodickou funkci f integrovatelnou na⟨0,T ⟩ konvergují Fourierovy koeficienty ak a bk k nule.
Teď se podíváme na operace. Nejprve jeden docela jasný výsledek, který vyplývá z toho, že koeficienty Fourierovy řady jsou dány integrály čili lineární procedurou.
Věta.
NechťT > 0, označmeω = 2π/T.
Nechť c je libovolné reálné číslo, nechť f a g jsouT-periodické funkce integrovatelné na⟨0,T ⟩. Předpokládejme, že
Pak
Teď bychom rádi dostali podobné vzorce pro derivování a integrování. S
derivací je to snadné. Předpokládejme, že f je
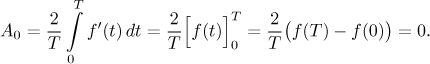
Integrály pro ostatní koeficienty se dají změnit v integrály, v nichž vystupuje f, pomocí integrace per partes.
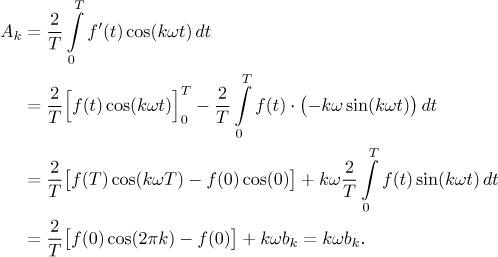
Podobně spočítáme bk a dostaneme následující tvrzení.
Věta.
NechťT > 0, označmeω = 2π/T.
Nechť f jeT-periodická funkce integrovatelná na⟨0,T ⟩. Předpokládejme, že
Pak
Vidíme tedy, že můžeme derivovat obě strany "relace tilda" (Fourierovu řadu člen po členu) a relace zůstane platná. Jak je to s rovností? Pokud použijeme obvyklé Jordanovy podmínky (ale aplikované na f ′), dostaneme následující implikaci.
Předpokládejme, že f je po částech spojitá s po částech spojitou první a druhou derivací. Pak
Takže můžeme konvergentní Fourierovu řadu derivovat člen po členu. Teď se
podíváme na integrování. Zase začneme formálním přiřazením Fourierovy řady,
takže budeme předpokládat, že f je
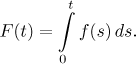
Teď uvažujeme nějaké t z intervalu
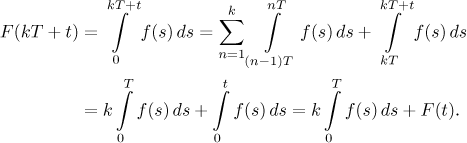
Vidíme, že tato primitivní funkce F je
Primitivní funkce k f jsouT-periodické přesně tehdy, kdyža0 = 0.
Za tohoto předpokladu se můžeme začít ptát na Fourierovu řadu přiřazenou k
F. Tentokráte jsou koeficienty dány integrály s F a my
použijeme integraci per partes k přechodu k integrálům s f, pak
použijeme periodicitu f a také fakt, že naše speciální F má
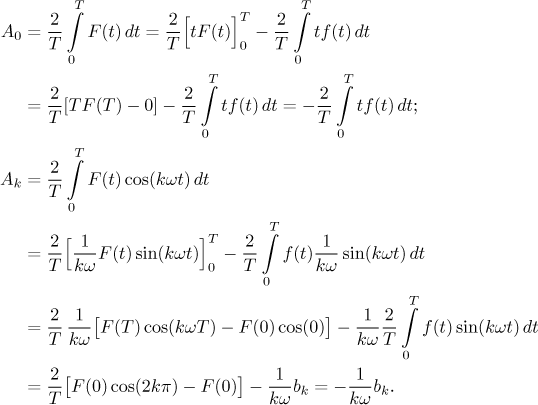
Podobně vypočítáme integrál pro Bk. Takto dostaneme následující tvrzení.
Věta.
NechťT > 0, označmeω = 2π/T.
Nechť f jeT-periodická funkce spojitá na⟨0,T ⟩. Předpokládejme, že
Jestliže a0 = 0, pak pro primitivní funkci danou
máme
Toto nám vypovídá o jedné konkrétní primitivní funkci. Jiné primitivní funkce se liší o konstantu, takže když uvažujeme množinu všech primitivních funkcí (neurčitý integrál), můžeme výsledek zapsat takto:
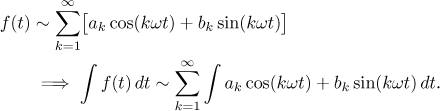
Jak to vypadá s rovností namísto formálního přiřazení? Zase použijeme Jordanovy podmínky. Potřebujeme zajistit, že existuje primitivní funkce, pro což je přirozeným předpokladem, že f je spojitá. Primitivní funkce F v předchozí větě je pak také spojitá, proto F a její derivace f splňuje "lepší" verzi předpokladů Jordanovy věty a dokonce dostaneme stejnoměrnou konvergenci.
Namísto formálního vyjádření našich úvah zkusíme něco jiného, podíváme se na
určitý integrál (což je v jistém smyslu obecnější). Protože nebudeme
pracovat s primitivními funkcemi, nebudeme se muset strachovat o jejich
periodicitu a tudíž nepotřebujeme požadavek, že
Věta.
NechťT > 0, označmeω = 2π/T.
Nechť f jeT-periodická funkce, která je po částech spojitá a integrovatelná na⟨0,T ⟩. Předpokládejme, že
Pak pro libovolné a < b máme
Teď se podíváme, jak Fourierova řada reaguje na transformace f. Všimněte si, že když je f periodická funkce, pak obvyklé transformace zase vedou na periodické funkce, a s výjimkou změny měřítka se dokonce i zachová původní perioda.
Věta (transformace).
NechťT > 0, označmeω = 2π/T.
Nechť f jeT-periodická funkce, která je integrovatelná na⟨0,T ⟩. Předpokládejme, že
Pak pro libovolné nenulové reálné číslo c máme
První tvrzení už jsme viděli, plyne s linearity. Všimněte si, že
a0 je vlastně průměr f (násobený dvakrát), takže
změnou měřítka proměnné (zmáčknutí nebo roztáhnutí grafu ve směru osy
x) nebo posunem funkce ve vodorovném směru se tento průměr
nezmění. Když ale funkci posuneme nahoru či dolů, tak se průměr příslušným
způsobem změní. Tím se vysvětlí, co se v těch vzorcích děje s
a0. Ostatní koeficienty říkají, jak důležité jsou
jednotlivé frekvence pro f, což se nezmění, když se funkce posune ve
svislém směru či změníme měřítko proměnné, ale změnou měřítka pro hodnoty
funkce evidentně změníme důležitost frekvencí. Poslední výraz je poněkud
komplikovanější, protože posunujeme "vlny v f" doleva či doprava,
ale siny a kosiny napravo se neposunují, což věci poněkud ztěžuje. Všimněte
si ale, že pokud je c násobkem základní periody T, tak ty
vzorce vlastně říkají, že
Poznamenejme, že poslední vzorec vypadá lépe v komplexním tvaru, viz níže.
Základní Fourierovu řadu lze přepsat, aby lépe vyhovovala různým potřebám. První přepis, který zde ukážeme, používá fintu, která je docela populární při práci s vlnami (signály, elektrické obvody atd.). Jsou-li dána čísla a a b, existuje jistý úhel φ a číslo A takové, že pro libovolné x máme
![]()
Číslu A se říká amplituda a úhlu φ se říká fázový úhel, jsou dány následujícími vzorci.
![]()
Pokud v definici φ prohodíme sinus a kosinus, tak dostaneme podobnou redukci, ale tentokráte s kosinem napravo (fázový úhel teď bude jiný). Pokud toto aplikujeme na všechny členy Fourierovy řady, dostaneme následující vzorce.
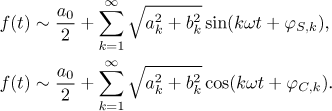
Zde použijeme jiný trik. Pokud ve Fourierově řadě nahradíme siny a kosiny jejich ekvivalentním vyjádřením pomocí exponenciál, dostaneme
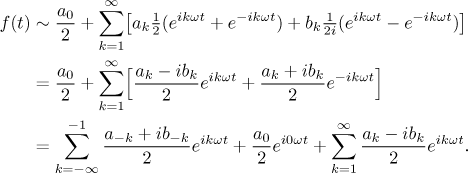
Když tedy označíme
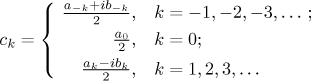
dostaneme komplexní tvar Fourierovy řady
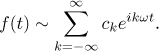
Toto je ve skutečnosti přirozený tvar této řady, protože pak mnoho vzorců vypadá lépe. Nemusíme například hledat ck přes několik případů, existuje společný vzorec pro všechny:
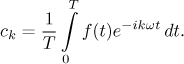
Je to tak, například pro kladná celá čísla k máme
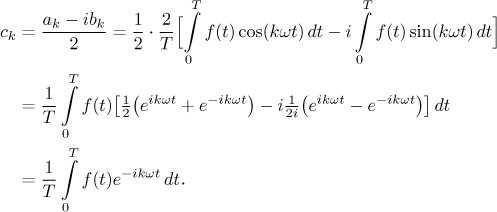
Podobně existují příjemnější formy pro vyjádření transformačních pravidel diskutovaných výše.
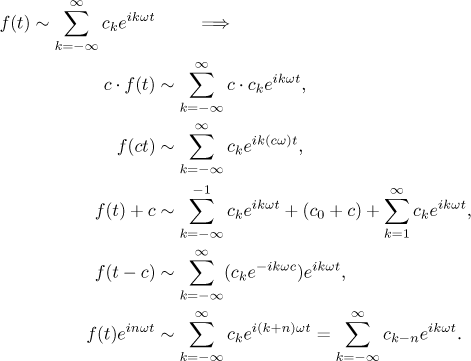
V posledním vzorci je evidentně n nějaké celé číslo.
Kdybychom zašli trochu dál tímto směrem, dostali bychom se k pojmu Fourierovy transofrmace, což už je ale jiná pohádka, tak raději skončíme.