Aplikace řad

Aplikací je samozřejmě spousta, ale mnoho z nich je příliš pokročilých a na úrovni, na které zde jsme, bychom je ani nemohli začít popisovat. Řady mohou například pomoci při řešení diferenciálních rovnic, Fourierova řada byla dokonce vyvinuta právě pro tento účel, ale na to si musíte počkat na nějaký kurs diferenciálních rovnic. Zde se podíváme na několik aplikací, které jsou buď snadnější, nebo alespoň jdou trochu rozumně popsat. Začneme obecnou myšlenkou použití Fourierových řad pro frekvenční analýzu (dokonce se tam zmíníme o mp3). Pak přejdeme k mocinným řadám. Začneme několika příklady, kdy nám pomohou s výpočty, odtud se přirozeně dostaneme ke gaussovskému integrálu. Mohlo by se namítnout, že to jsou spíš věci historické než současné, a tak se podíváme na výpočet funkcí, což je něco, co používáte pokaždé, když zmáčknete knoflík na kalkulačce nebo chcete nějaký výpočet po počítači. Na závěr se rychle podíváme na hledání pí.

Fourierova řada a frekvence

Základní myšlenka Fourierových řad je, že danou funkci vyjádříme jako kombinaci oscilací, počínaje tou, jejíž frekvence je dána zadanou funkcí (buď její periodicitou nebo délkou omezeného intervalu, na kterém je zadána), a pak se berou násobky této frekvence čili používáme dělených period. Když se podíváme na koeficienty výsledné "nekonečné lineární kombinace", tak můžeme čekat, že když je nějaký výrazně větší než ostatní, tak tato frekvence hraje významnou roli v jevu popisovaném naší funkcí. Tato detekce skrytých period může být velice užitečná v analýze, protože ne každou periodicitu dokážeme z funkce hned vykoukat. Platí to obzvláště v případech, kdy se skládá několik různých period.

Představte si, že funkce f popisuje teplotu v čase t po mnoho a mnoho let. Jednu periodu bychom měli vidět hned, jmenovitě změny s ročním obdobím v průběhu jednoho roku. Na této základní roční periodě očekáváme další přidanou periodu, jmenovitě jednodenní periodu chladných nocí a teplých dnů. Opravdu zajímavá je otázka, jestli tam jsou i jiné periody. To může být velmi užitečné, protože by nám to řeklo něco důležitého o vývoji počasí a klimatu. Frekvenční analýza nabízí nástroj pro takoé zkoumání, při aplikaci na dlouhé časové řady může vypíchnout doby ledové a další dlouhodobé změny klimatu.

Jsou oblasti, kde se rozklad na vlny objevuje přirozeně, například při ukládání zvuku. Když dostaneme zvukový vzorek, Fourierova transformace nám umožňuje jej rozložit na základní vlny a uchovat v tomto tvaru. Kromě datové komprese ušetříme ještě další místo tím, že prostě ignorujeme koeficienty příslušející frekvencím, které typické lidské ucho neslyší. Tak vypadá základ formátu mp3 (používá transformaci, která je něco jako potomek čtvrté generace kosinové Fourierovy řady).

Fourierův rozklad je také možno zobecnit na více dimenzí a pak je docela dobrý na uchovávání obrazové informace - je například srdcem systému používaného FBI k uchovávání databáze otisků prstů. Protože je tento rozklad tak užitečný, důležitým faktorem se stává rychlost, jakou jsme schopni hledat koeficienty. To se stalo inspirací pro další vývoj a dnes obvykle nepoužíváme Fourierovu řadu, ale nějakého jejího mocnějšího potomka, například něco zvané Fast Fourier Transform (FFT, Rychlá Fourierova transformace). Zde přispívá i hardware, existují mašinky (integrátory), které už mají tohle zadrátováno, zhruba řečeno se do toho strká funkce a ono to vyplivuje Fourierovy koeficienty.

Abychom to nějak uzavřeli, Fourierův rozklad potkáváte pokaždé, když posloucháte něco v mp3 (popřípadě když vám policie bere otisky prstů).

Než se objevily kalkulačky, byly mocninné řady ne jen důležité, ale naprosto zásadní. Při výpočtech se všechny funkce nahrazovaly Taylorovými řadami, popřípadě jejich konečnými částmi - polynomy. Inženýři si dřív pamatovali rozvoje mnoha funkcí a běžně je používali. Například namísto následujícího výpočtu limity pomocí l'Hôpitalova pravidla

se dá udělat tento trik, který by zkušený inženýr dělal z hlavy (viz tento příklad v části Řešené příklady - Řady funkcí).

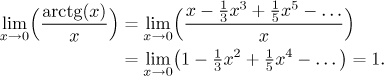
Samozřejmě bez stejnoměrné konvergence to může být docela nejisté, ale zde ji máme. Potkal jsem jednou limitu, která v sobě měla nepříjemný součin, takže po použití l'Hôpitalova pravidla narostla, po čtyřech l'Hôpitalech už se výraz nevešel na řádek a vzdal jsem to. Pak jsem nahradil všechny sin(x) řadou a bylo to hotovo skoro hned.

Další příklad: Pokud chceme vědět, jaká je násobnost čísla x = 0 coby kořene f (x) = 1 − cos(x), tak to můžeme zkusit podle definice, nebo uděláme toto:

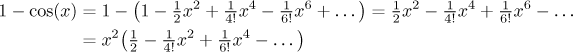
a násobnost je jasná.

To byly triviální příklady, ale podobné triky pomáhají také ve složitějších výpočtech. Jedna zajímavá příhoda jde zpět do dob Druhé světové války. Vývoj atomové bomby vyžadoval velice komplikované výpočty, které si pomocí řad zjednodušili na spoustu sčítání a násobení. Problém se pak vyřešil tak, že nacpali halu plnou (mechanických!) sčítacích a násobících strojů a vymýšleli geniální způsoby, jak jimi výpočty prohánět. Pro další počtení silně doporučuji Feynmannovy paměti.

Přinejmenším 90 procent všech statistických výpočtů je založeno na tom, že známe takzvané "normální rozdělení", což v zásadě znamená, že potřebujeme vědět, kolik je integrál

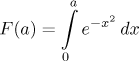
pro kladná a. Bohužel je známo, že primitivní funkce k f (x) = e^−x2 existuje, ale nelze ji vyjádřit pomocí elementárních funkcí a obvyklých operací (včetně skládání). Jsou dvě možnosti, jak tento problém obejít. Jedna možnost je použít numerickou aproximaci onoho určitého integrálu, ale to by se muselo dělat pro každé a z rozumně husté množiny, což je docela dost práce. Druhá možnost je najít výraz pro F(a) a pak jej přímo vypočítat. Řady nabízejí pěkný způsob, jak to udělat. Začneme rozvojem exponenciály.

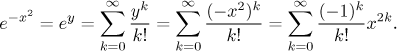
Teď integrujeme.

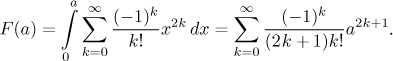
Tato řada konverguje pro všechna a, takže spočítáme tolik členů, kolik potřebujeme na žádanou přesnost. Protože to lidé pracující ve statistíce potřebují docela hodně, tyto hodnoty byly shromážděny v tlustých knihách distribučních tabulek a taky byly vyvinuty algoritmy pro statistický software.

Podobný výpočet pomůže řešit tento příklad v části Integrály - Řešené příklady - Integrály.

Lidský mozek a procesory umí dělat základní algebraické operace - sčítání, násobení, odčítání a (s trochou úsilí) dělení. Pokud chceme hodnotu, kterou nelze získat kombinováním těchto základních operací, tak máme průšvih a mají ho také kalkulačky/počítače. Jak spočítáme pátou odmocninu z 2? Jak dostaneme ln(3)? A co e^2.9?

Přirozenou odpovědí jsou řady. Máme například pěknou řadu pro exponenciálu. To ale přináší jiný problém. Kalkulačka potřebuje vědět, kolik členů řady má spočítat, ale řada konverguje pomaleji pro větší x. Naštěstí nám pomůže jednoduchý algebraický trik. Napíšeme x jako x = n + r pro celé číslo n a nějaké číslo r z intervalu ⟨0,1). Víme, že

e^x = eⁿ⋅e^r = e⋅e⋅e⋅...⋅e⋅e^r.

Protože násobení není problémem a samotné číslo e je někde schováno, tak vidíme, že stačí umět najít e^r pro r < 1. Řada pro exponenciálu už na intervalu ⟨0,1) konverguje stejnoměrně, takže máme její konkrétní oříznutí, které dává dobrou aproximaci pro všechna taková r.

Logaritmus je podobný případ, máme řadu, ale teď není hlavním problémem rychlost. Řada pro logaritmus dokonce ani nekonverguje pro velká x, můžeme ji použít pouze pro x < 2. Zde použijeme následující algebraické zjednodušení. Napíšeme x jako x = 2ⁿ⋅r pro celé číslo n a nějaké číslo r z intervalu ⟨1,2). Víme, že

ln(x) = nln(2) + ln(r).

Zase vidíme, že vlastně stačí umět logaritmus malých čísel, pro což už máme řadu.

Zde se často používá jiný trik k urychlení výpočtu. Pro logaritmus máme více řad a tyto dvě vypadají podobně.

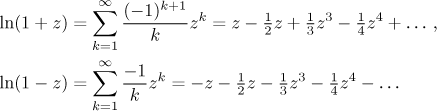
Když je odečteme, dostaneme zajímavý vzorec.

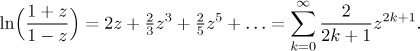
Tato řada konverguje mnohem rychleji, protože přeskakuje každý druhý člen. Výpočet pak funguje následovně. Nejprve rozložíme x na n a r jak bylo naznačeno výše. Pak najdeme z takové, že

Nakonec spočítáme tu rychlou řadu výše. Omezení na r (bereme jen čísla mezi 1 a 2) znamená, že z se bere z intervalu ⟨0,1/3) a tam řada konverguje stejnoměrně, takže zase víme, jak dlouhé částečné součty potřebujeme k dostatečně dobré aproximaci pro všechna tato z.

Jakmile máme logaritmus a exponenciálu, můžeme pomocí nich hledat další věci, například obecnou mocninu A^B.

Pí je transcendentní číslo, což znamená, že jej nemůžeme vyjádřit pomocí algebraických operací. Jeden způsob jeho vyčíslení nabízí řady. Pokud použijeme řadu pro arkus tangens, kterou už jsme viděli výše, dostaneme

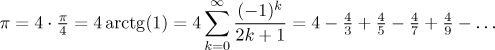
Můžeme sečíst kolik chceme členů této řady, abychom dostali potřebnou přesnost. Tato řada je ve skutečnosti dosti špatná, protože konverguje velice pomalu; na urychlení její konvergence se používá spousta triků.

Podobně rozvoj exponenciály nabízí způsob, jak najít hodnotu e.

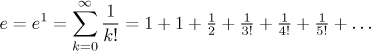
Protože toto je v jistém smyslu poslední sekce Math Tutoru, myslím, že si ji mohu dovolit zakončit příhodou. Když jsem byl na gymplu, objevil se problém s krádežemi v šatně a studenti drželi hlídky. Jednoho dne na mne přišla řada, měl jsem tam s kamarádem sedět několik dlouhých hodin a v zásadě nic nedělat. Oba jsme sdíleli postižení zvané láska k matematice, a tak jsme se rozhodli spočítat e na 50 desetinných míst. Vzali jsme si dva velké kusy papíru a jeden fungoval jako "dělič", druhý jako "sčítač".

"Dělič" začal s 1 na prvním řádku. Vydělil to 2 a dostal řádek s 0.5000. Na dalším řádku to vydělil 3, čímž dostal 0.16666666666666... (padesát míst). Tímto způsobem pokračoval, na každém řádku tak bylo číslo 1/k! potřebné pro řadu.

"Sčítač" začal s 1, pak přičetl první řádek z děličova papíru, pak druhý, a tak dále. Když dělič dospěl k řádku s padesáti 0, byli jsme hotovi. Tímto způsobem jsme ty nudné hodiny přečkali. Nakonec jsme v nějaké knize našli "oficiální" hodnotu e a ukázalo se, že jsme někde okolo 30. destinného místa udělali chybku. Než se objevily mechanické počítačky, tak se přesně takto dělaly výpočty, stovky lidí zvaných "kalkulátoři" seděli ve špatně osvětlených místnostech a trávili své životy nudnými výpočty. Pro nás to byla zajímavá zkušenost.

Zpět na Teorie - Řady funkcí