Sčítání mocninných řad: Přehled metod

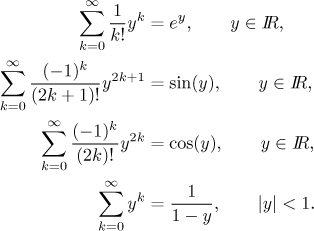
Je dána řada funkcí ∑ f_k(x) a chceme najít její součet (pokud je to možné). Na to neexistují žádné obecné metody, ale jeden konkrétní přístup může často pomoci. Základní myšlenka je, že se danou řadu snažíme upravit tak, aby vypadala jako řada, kterou už známe - přičemž je nutno vzít v úvahu možnost použít substituci. Ve většině případů toto používáme pro mocninné řady, ale substituce nám dovolí to použít i pro jiné řady (pokud máme štěstí).

Čím víc řad na začátku známe, tím lepší jsou šance na úspěch, ale obvykle jsou počátečním bodem tyto čtyři.

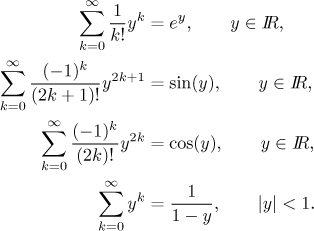
Je také dobré znát řady pro logaritmus.

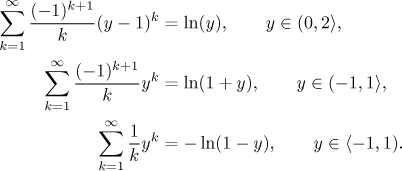
Dá se ale obejít bez nich, pokud jste ochotni víc pracovat: Takovéto řady lze převést na geometrické rozvoje pomocí derivace.

Algoritmus: Postup začíná tím, že se napíše rovnost, kdy na jednu stranu dáte danou řadu a na druhou stranu symbol f (x). Pak aplikujte rozličné transformace na obě strany této rovnosti, abyste z dané řady nakonec vytvořili řadu, kterou už znáte, tu můžete nahradit příslušnou funkcí. Nakonec vyřešte vzniklou rovnost pro f.

Jsou dvě věci, které je obvykle potřeba udělat.

Krok 1. Části f_k, ve kterých se vyskytuje x, by měly být napsány jako [g(x)]^k, kde g(x) je výraz, který je stejný pro všechna f_k. Základním nástrojem je závorkování a posun mocnin vytýkáním věcí z řady nebo jejich přesunem do řady. Několik jednoduchých příkladů:

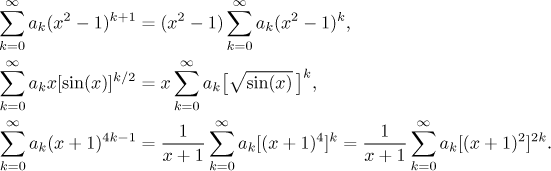
Všimněte si, že v posledním příkladě jsme nabídli dvě možnosti, protože tuto řadu je také možné naroubovat na řadu pro kosinus. Jestli je to dobrý nápad nebo ne záleží na koeficientu a_k. Pokud jej dokážeme přepsat tak, aby se ve jmenovateli objevily faktoriály (2k)! (viz následující krok), pak směřování ke kosinu může být dobrý nápad. Popřípadě k sinu - viděli jsme, že posunout mocninu o 1 nahoru či dolů není problém; vše záleží na koeficientech a na tom, co jsme tam schopni vytvořit. Obecně lze všechny členy s mocninou k přepsat jako členy s mocninou 2k či nějaký jiný násobek k a naopak, jak je tomu v předchozích příkladech; zde máme určitou svobodu a koeficienty by nás měly nasměřovat, viz další krok.

Krok 2. Je třeba upravit koeficienty tak, aby měly správný tvar. Je pět základních operací, které je možno použít.
• Pokud mají koeficienty tvar součtu, je možné rozdělit řadu na dvě.
• Nechtěné konstanty, které nezávisí na k, mohou být vytknuty.
• Výrazy A^k lze zahrnout do části s x.
• Výrazy jako k, k + 1 atd. ve jmenovateli lze odstranit, když se řada zderivuje - musí se ale upravit vhodně mocnina u x, posun se probral v Kroku 1. Pokud se například chce odstranit k − 1 ze jmenovatele, tak je nejprve třeba upravit skupinu s x tak, aby měla tvar [g(x)]^k−1, a pak derivovat.
• Výrazy jako k, k + 1 atd. v čitateli lze odstranit, když se řada zintegruje - zase se ale musí upravit vhodně mocnina u x. Pokud se například chce odstranit k − 1 z čitatele, tak je nejprve třeba upravit skupinu s x tak, aby měla tvar [g(x)]^k−2, a pak integrovat.
Není rozumný způsob, kterým by šlo přidat/odebrat faktoriály, takže pokud se objeví v dané řadě, tak už v zásadě rozhodnou, kterým směrem jít - všimněte si, že ty čtyři řady výše mají rozdílné typy faktoriálu.

Krok 3. Když má řada správný tvar, je třeba také zajistit, aby indexy začínay na správném místě, používá se na to trik s přičtením/odečtením (viz Úpravy (mocninných) řad v části Přehled metod - Řady funkcí).

Značení: Jsou v zásadě dva způsoby, kterými je možno to dělat. Obecný způsob je ten popsaný výše, kdy základní rovnici s řadou na jedné a " f (x)" na druhé straně upravujete, dokud nejste schopni řadu nahradit vzorcem. Tento způsob je ale někdy zbytečně komplikovaný. V případě, že chcete používat pouze operace, které řadu samotnou nemění, jen upravují (což hlavně znamená, že neplánujete derivovat a integrovat), tak můžete použít jednodušší zápis. Začnete danou řadou a pomocí řetězce rovností ji dostanete do známeho tvaru, který už umíte sečíst.

Teď ukážeme příklad. Je trochu ďábelský, protože chceme ukázat, co všechno se dá udělat. Pro rozumnější příklady se podívejte na Řešené příklady - Řady funkcí.

Příklad: Najděte součet řady

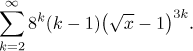
Protože tam nejsou faktoriály, tak tuto řadu nelze převést na řadu pro exponenciálu, sinus nebo kosinus. Zkusíme ji tedy přepsat tak, aby vypadala jako geometrická řada, použijeme obecné značení s  f diskutované výše. Nejprve se zbavíme té 3 v mocnině, pak přesuneme člen 8^k do části s x.

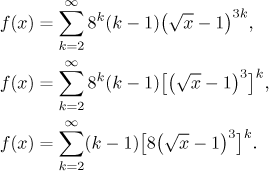
Teď se potřebujeme zbavit k − 1, takže si připravíme příslušnou mocninu a integrujeme.

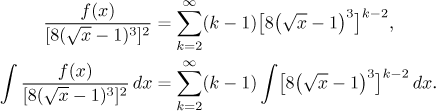
Vidíme, že integrál napravo neumíme, takže se musíme vrátit a připravit si řadu trochu opatrněji. Přidáme tam nějaké členy, které nám umožní použít pro integraci přirozenou substituci.

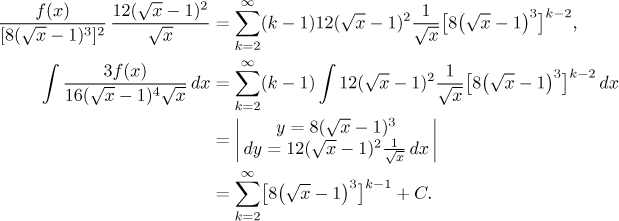
Teď zase upravíme mocninu u x-ového členu a pak použijeme vytýkací fintu, díky které začne indexace této geometrické řady od 0. Pak už lze použít geometrický rozvoj.

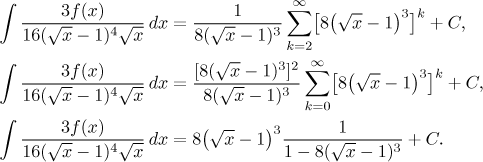
Připomínáme, že geometrický rozvoj platí jen tehdy, když jsou členy umocňované na k menší než 1 v absolutní hodnotě. To určí platnost výsledku. Teď zbývá vyřešit pro f.

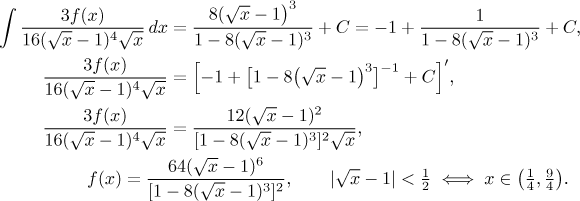
Mimochodem, na první řádce jsme udělali následující: Celou třetí mocninu jsme si označili jako A, pak jsme použili můj oblíbený trik přičtu/odečtu.

Poznámka: Samozřejmě, pro mnohé řady tyto triky vůbec nepomůžou. Někdy fungují dobře a dají nám pěknou řadu, ale potíže nastanou později, když řešíme pro f. Jako příklad stručně ukážeme jednu řadu, která předstírá, že je snadná, a kterou bychom opravdu rádi uměli sečíst.

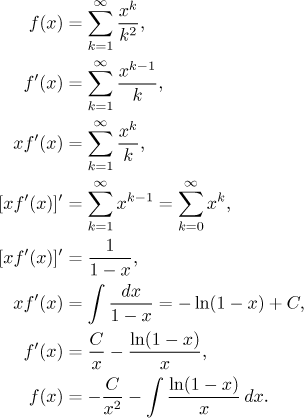
A to je konec, nevíme, jak explicitně vyjádřit ten integrál na posledním řádku.

Rozvoj v Fourierovu řadu
Zpět na Přehled metod - Řady funkcí