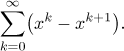
Zde zkusíme aplikovat standardní testy a určit konvergenci řady

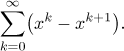
Budeme považovat x za parametr a sčítáme vzhledem ke k. Jaké testy můžeme použít? Srovnání se zdá mimo, protože pro velká k nejde nic ignorovat. Je tedy pravda, že výraz k + 1 vypadá v zásadě jako k pro velké hodnoty k, ale toto se děje v exponentu mocniny a tudíž toto zjednodušení nelze použít, my totiž víme, že to funguje jen ve zlomcích. Mimochodem, kdybychom to zkusili i zde, dostali bychom

To by ukazovalo, že tato řada konverguje pro všechny hodnoty x, což je ovšem špatně, viz níže.

Takže srovnání nepomohlo, což takhle populární dvojčata, odmocninové a podílové kritérium? Začneme odmocninovým kritériem.

Vidíme, že daná řada konverguje absolutně na intervalu (−1,1). Stejný závěr dostaneme pomocí podílového kritéria.

Víme také, že pro |x| > 1 naše řada diverguje, zde použijeme verzi odmocninového kritéria pro obecné řady, viz např. poznámku na konci sekce Odmocninové a podílové kritérium v části Teorie - Testování konvergence.

Dalo by se to také dokázat přímo. Nejprve přepíšeme členy řady takto:

|a_k| = |x|^k⋅|1 − x|.

Teď vidíme, že pro |x| > 1 jdou členy |a_k| do nekonečna, tedy a_k nejdou k nule.

Zbývá individuálně vyšetřit body x = −1 a x = 1, ale to už jsme dělali.