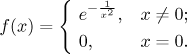
Zde prozkoumáme Taylorovy věci pro funkci
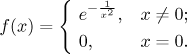
Řekněme si hned zkraje, že tato funkce není ani divná, ani škaredá, je to
pěkná funkce. Konec konců, výraz v definici je jen složení eponenciály
(nejlepší funkce) a mocniny, na vzorečku
Když se zeptáme na obvyklé vlastnosti, tak zjistíme, že tato funkce má v zásadě všechny, je to skoro nejhezčí možná funkce, protože má všude spojité derivace všech řádů. Protože to ještě bude důležité, tak naše tvrzení dokážeme a dokonce dáme přesnější vyjádření tohoto výsledku.
Tvrzení.
Pro každé přirozené číslo k existuje polynomPk(x) stupně nanejvýš2k − 2 takový, že pro nenulové x máme
Taková tvrzení se obvykle dokazují matematickou indukcí.
k = 1: Najdeme obvyklým způsobem první derivaci a jen z zvědavosti i druhou.
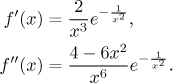
V obou případech to funguje, vzorec je přesně jak jsme tvrdili.
Teď bychom měli udělat indukční krok. Předpokládejme, že Tvrzení platí pro
k, a ukážeme, že pak také musí platit pro
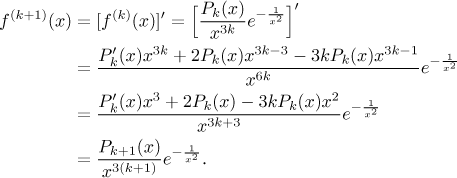
Podle našeho předpokladu je
Odhad stupně čitatele je důležitý z následujícího důvodu. Nám vlastně stačí
vědět, že jeho stupeň je menší než stupeň jmenovatele, takže když ten
polynom vydělíme, zůstanou tam jen členy typu
Tvrzení.
Pro každé přirozené číslo k máme
Stačí totiž použít substituci
![]()
Opakované použití l'Hôpitalova pravidla pak dává nulu, viz škála mocnin, podobně vypočítáme limitu zleva. Tato substituce také zjednoduší derivování f, viz Poznámka na konci.
Toto tvrzení ukazuje, že funkce f má také derivace všech řádů v počátku a jsou rovny nule. To znamená, že graf této funkce je v počátku extrémně plochý. Připomeňme, že když chceme najít Taylorův polynom/Taylorovu řadu se středem 0, tak k nalezení koeficientů používáme přesně tyto derivace. Dostaneme proto následující závěr.
Fakt.
Uvažovaná funkce f má Taylorovy polynomy všech stupňů se středema = 0 a Taylororovu řadu se středema = 0 a
Co to znamená? Za prvé, protože daná funkce je mimo počátek nenulová, tak (s výjimkou středu 0) Taylorovy polynomy neaproximují dobře původní funkci f, vlastně ji neaproximují vůbec. A to navzdory tomu, že f je hladká, s derivacemi všech řádů všude, takže z běžného úhlu pohledu je "pěkná".
Co se týče řady, Taylorovy polynomy konvergují - coby částečné součty této řady - stejnoměrně na celé reálné ose k T. Tato řada je tedy zase nejlepší možná, ale rozhodně se nerovná původní funkci f. Připomeňme, že jsme měli větu, která zaručovala dobrou konvergenci řady v případě, že f má na nějakém okolí stejnoměrně omezené derivace. To zde tedy evidentně neplatí, neexistuje okolí 0, na kterém by derivace byly stejnoměrně omezené.
Toto ukazuje, že problém aproximace funkcí mocninnými řadami může být docela zákeřný i pro pěkné funkce.
Poznámka:
Substituce
y′ = −1/x2 = −y2.
Teď jen aplikujeme řetízkové pravidlo a zjistíme, že
f ′(x) = [e−y2]′ = (−2ye−y2)⋅y′ = 2y3e−y2.
Podobně
f ′′(x) = [2y3e−y2]′ = (6y2 − 4y4e−y2)⋅y′ = (4y6−6y4)e−y2.
Když do toho dosadíme