Problem: Investigate convergence of the following sequence of functions:
![]()
Solution: First we investigate pointwise convergence. We treat x as a parameter and evaluate limit with respect to k. We see that the nature of this limit depends on the value of x:
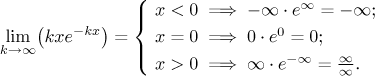
Thus we see that this sequence diverges for negative x. For positive x we use l'Hôpital's rule (note that x is a parameter, so we start pretending that k goes through real numbers and differentiate with respect to this k).
![]()
Conclusion: The given sequence converges to the function
How about uniform convergence? We start by investigating the difference between f and a particular fk on the above region of convergence.
![]()
We find this global maximum in the usual way, we identify suspicious points and compare values/limits at them (now k is a fixed parameter and we use x as the working variable).
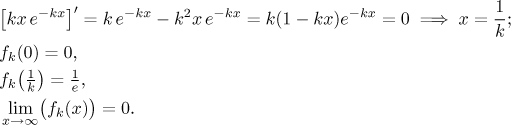
We see that
![]()
We see that the distance between the limit f and the terms of the sequence fk stays large when viewed globally over the whole region of convergence, so we do not have arbitrarily good approximations of f by fk on this set. In other words, the pointwise convergence that we determined above is not uniform. Computer printout agrees well with our theoretical results.
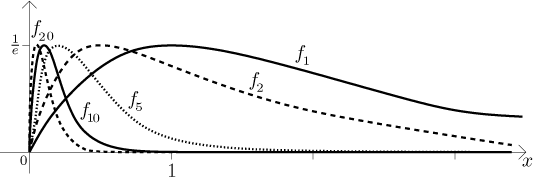
If we fix some positive x, then the functions
fk at this point go to 0 (and it seems that quite
fast). On the other hand, we see a hump of constant height that glides left
toward the origin (we determined that the maximum happens at
Fix any a > 0, consider the set
![]()
We easily check that Mk goes to 0 as k goes to infinity, which proves uniform convergence on the set M.
Conclusion: The given sequence converges to the function 0 uniformly
on every set of the form