Problem: Investigate convergence of the following sequence of functions:

Solution: First we investigate pointwise convergence. We treat x as a parameter and evaluate limit with respect to k. Since the sine in the numerator is bounded by 1 in absolute value and the denominator goes to infinity, we get

Formally one could use for instance comparison.

Conclusion: The given sequence converges to the function f (x) = 0 on the whole real line (which is thus the region of convergence of this sequence).

How about uniform convergence? We start by investigating the difference between f and a particular f_k on the above region of convergence.

We have just proved uniform convergence.

Conclusion: The given sequence converges to the function 0 uniformly on the whole real line.

I asked the computer for a few graphs just to show the general idea of what is happening here.

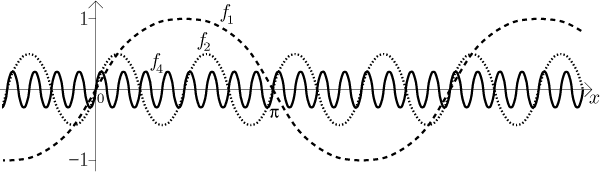
This example is so simple that you probably wonder why are we showing this; there surely is something more to this problem. And there is, which we quickly find once we try to differentiate.

With exception of point x = 0 this sequence of derivatives does not even converge as k goes to infinity, in particular it does not go to 0, that is, to f ′.

To sum up, we have functions f_k that converge uniformly to f on any subinterval of the positive half-axis, but f_k′ do not converge to f ′ on any such interval, not even pointwise. This shows that differentiating convergent series may be really tricky.

Next problem
Back to Solved Problems - Series of functions