Box "comparison and oscillation"

There are several ways to use comparison to find limits. There are two one-sided comparisons possible:

Consider two functions f and g such that f ≤ g on some reduced neighborgood of a.
If f →∞ at a, then also g→∞ at a.
If g→−∞ at a, then also f →−∞ at a.

Another comparison with two functions uses absolute value, it is the absolute value version of the Squeeze theorem:

Consider two functions f and g such that | f | ≤ g on some reduced neighborgood of a.
If g→0 at a, then also f →0 at a.

To obtain non-zero limits by comparison, one needs two bounds:

The Squeeze theorem:
Consider three functions f, g, and h that satisfy f ≤ g ≤ h on some reduced neighborhood of a. If f converges to some L at a and h converges to the same L at a, then also g converges to L at a.

For details see the section Limit and comparison in Theory - Limits. All statements also work for one-sided neighborhoods and one-sided limits.

The above statements about comparison are used most often for one of the following two reasons:

Reason 1. The expression we are investigating features an expression that does not have a limit but is bounded - that is, an expression that oscillates. The most typical examples are sine and cosine at infinity.

Example: We will show that

Substituting infinity does not help, since sine does not have a limit and therefore we cannot use the limit algebra. However, the sine is bounded by −1 and 1, which suggests a squeeze:

for x > −1, that is, on a neighborhood of infinity.

The function on the left converges to 1 at infinity:

The function on the right also goes to 1 at infinity (it is a constant function 1), therefore by the Squeeze theorem, the given function converges to 1 at infinity. We can express out reasoning as follows:

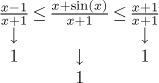
Reason 2. Sometimes comparison allows us to simplify expressions and so avoid more complicated methods.

Example: We know that for x > 1 we have

At infinity, the expression on the right goes to infinity, therefore by comparison also the expression on the left goes to infinity there. If we wanted to use direct calculation to determine the limit of the expression on the left at infinity, we would have to apply the l'Hospital rule, which most likely would not be very nice, or use a rather complicated factoring out of dominant terms.

Using comparison proceeds in two steps:

Step 1. Find some comparison(s) (that is, bound(s)) for the given function. Oscillating but bounded terms have natural bounds which can be used to derive bounds for the whole function algebraically (as in the first example). Often we get bounds also by ignoring parts of the given expression (as in the second example).

Step 2. Find the limit of the bound(s). Then check whether any conclusion is possible by any of the above comparison statements. Remember that the Squeeze theorem requires that both bounds converge to the same limit.

In Solved Problems - Limits, these methods are used in this problem, this problem, and this problem.

Next box: nice outer function
Back to Methods Survey - Limits