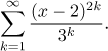
Problem: Sum up the following power series.
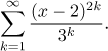
Solution: We need to convert the given series into a series that we already know. Since there is no factorial in this series and we do not know any tricks for somehow creating it there, we will not be able to use the series for the exponential, sine and cosine. Thus we turn our attention to the geometric series (or logarithmic or binomial series, if we happen to remember them). Since the given series consists solely of powers with exponent k (there is also 2k, but that we fix easily), the geometric series is the obvious choice. To make the given series look accordingly, we first remove the extra "2" from the exponent by hiding it inside and then it is easy. Since we will be only using algebraic operations, we can write our work using the easier way - a chain of equalities.
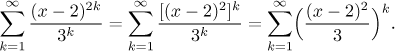
Almost there, the last thing missing is that we start our indexing at 1, but the geometric expansion starts at 0. The general trick here is to add the missing term (and then subtract it to make things equal).
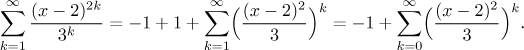
Now we are ready to sum the given series up, we do not forget that the summation is true only on the region of convergence of the series that we use.
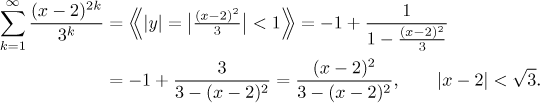
For the geometric series we also have another way to fix the indexing, by factoring out the term with the lowest power present in the series.
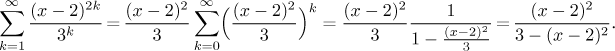
This approach typically yields more friendly formulas. This is no surprise, a method that is specific to the given situation usually works better than a general one.