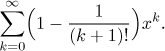
Problem: Sum up the following power series:

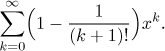
Solution: We do not know any series whose coefficients would consist of several parts, so we first need to somehow handle this problem. There are essentially two ways. We could try to rewrite each coefficient as one term and then take it from there. The other option is to split the series into two. What would be the better choice? When we picture the outcome of merging the two parts of a coefficient (using common denominator), we see that it is definitely not something that we would want to mess with. On the other hand, the individual parts in that difference are really nice, so this second approach is definitely better.

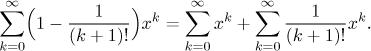
The first series is simple to sum up, since it is a geometric series.

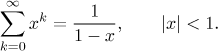
Now we will look at the second series. We need to turn it into some series that we already know. Since it contains all powers, the sine or cosine series do not seem like a good idea, and since we do not know how to get rid of factorials, we are left with a series that features all powers and also factorials: The exponential series.

The only trouble is that we do not have exactly k! in the denominator. This can be handled in two different ways. First, we can shift the indexing.

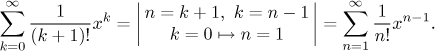
Now we have two problems, the power and the first index do not fit. The power can be easily changed when we divide and multiply this last series by x, the missing first term in the exponential series can be filled in using the add-subtract trick. As usual we will use the traditional k instead of n. Since we will only be using algebraic operations, we will write it using the easier way - a chain of equalities.

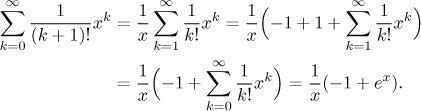
We have little trouble at 0, but this is no problem. The question reads "sum up the series", so we simply put 0 into the given series and get the answer that way.
Conclusion:

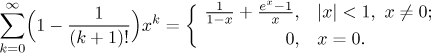
Alternative:
What is the other way in which we can work out the second series? Our problem is the factorial of k + 1, we would prefer the factorial of k. It will appear there if we create k + 1 in the numerator, and for that we have a trick: differentiation. Namely, we would need to differentiate x^k+1, which we easily create by multiplying the given series by x. Note the following thing. In the first solution above we started with the given series and via a chain of equalities we changed it into a form that we were able to sum up. Here it is not possible, because we want to differentiate, that is, we want to pass to a different object that is not equal to the given series (or its rewritten version). Therefore we need to use a different notation for our calculations, the one with f.

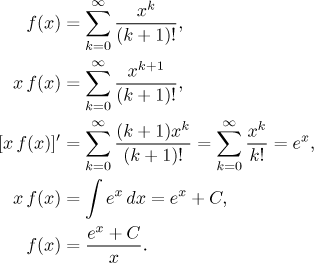
What is C? The usual way to find out is to put some number for x on both sides of the last equality, and recall that f stands for the given series. When we look at it, we see that the only x for which we can evaluate this series is x = 0, but this number cannot be substituted into the expression on the right. Can we put it into the second last line, before we divided by x? Actually, not again, but for a different reason. Recall that we are allowed to multiply an equality by a number only if it is not zero - however, when x = 0 then on the second line we do exactly that. This means that the solution that we presented, starting from the second line, only works for non-zero x.

To get out of this situation we need to apply some knowledge of functions. When we look at the second last line, we see equality between two functions that is true on an interval except a point in its middle, namely they are equal on some reduced neighborhood of 0. Therefore these two functions have to have the same limit at 0, and because they are continuous, they have to be equal at 0. Thus we conclude that the second last line can be also used when x = 0. When we substitute it in, we get C = −1, therefore we obtain the same formula as in the first solution.

Next problem
Back to Solved Problems - Series of functions