Elementární teorie množin

Zde stručně připomeneme základní pojmy o množinách. Protože se v této sekci hlavně snažíme připomenout značení, nebudeme příliš rigorózní.

Množinou obvykle míníme nějakou skupinu objektů. Při značení používáme malá písmena pro prvky množiny a velká pro množiny. Pokud prvek a náleží do množiny A, zapisujeme to a∈A. Pokud tento prvek nenáleží do této množiny, značíme to a∉A.

Vždy pracujeme v určitém světě, zvlášť pokud máme více množin, pak potřebujeme vědět, jaké je univerzum množin, ze kterého čerpáme prvky pro naše množiny. Toto univerzum obvykle značíme U. Typická množina v takovémto vesmíru je daná nějakou podmínkou, množina pak jsou všechny body z tohoto univerza, které danou podmínku splňují. Pokud je podmínka označena φ s hodnotami platí/neplatí, pak je taková množina zapsána jako

A = {a∈U; φ(a)}.

Příklad: Ve vesmíru U všech lidí se množina mužů zapíše jako

A = {a∈U; a je muž}.

Poznamenejme, že tento intuitivní přístup může stačit pro běžnou práci, ale má v sobě dost velké problémy (viz tato poznámka). Proto se při vážnější práci s množinami musí množiny dělat komplikovaněji. To nás tady ale nebude trápit.

Než popojdeme dál, připomeňme, že je jedna speciální množina, která funguje ve všech vesmírech, jmenovitě prázdná množina O = {}, množina bez prvků.

Porovnávání množin.

Dvě množiny jsou shodné, pokud mají stejné prvky. Používáme na to normální znaménko rovnosti A = B.

Uvažujme množiny A a B ve vesmíru U. Řekneme, že A je podmnožinou B, značeno A⊆B, jestliže je každý prvek A také prvkem B.

Všimněte si, že toto také dovoluje množinám, aby se rovnaly. Mimochodem, prázdná množina je podmnožinou libovolné množiny.

Relace býti podmnožinou se nazývá inkluse. Pokud jsou dvě množiny navzájem podmnožinami, pak musí být nutně stejné.

Operace s množinami.

Doplněk. Je-li dána množina A ve vesmíru U, definujeme její doplněk jako

A^c = {a∈U; a∉A}.

Všimněte si, že doplněk závisí na vesmíru, ve kterém pracujeme. U dalších operací níže už tak podstatný není.

Sjednocení. Jsou-li dány množiny A a B ve vesmíru U, definujeme jejich sjednocení jako

A ∪ B = {c∈U; c∈A nebo c∈B}.

Poznamenejme, že pokud jsou A a B konečné množiny, tj. množiny s konečně mnoha prvky, pak je jejich sjednocení také konečná množina, ale počet jejích prvků nemusí být součtem jednotlivých velikostí. To je způsobeno tím, že množina obsahuje každý prvek pouze jednou, takže když přidáme jeho kopii, tak jakoby splyne s tím prvkem, který už tam je. Například množina {a,a} a množina {a,a,a,a} mají obě stejnou velikost, protože jsou rovny množině {a}. Teď už by nemělo překvapit, že když sjednotíme {a,c,r} s {b,c,r} (množiny velikosti 3), dostaneme množinu velikosti 4 {a,b,c,r}.

Průnik. Jsou-li dány množiny A a B ve vesmíru U, definujeme jejich průnik jako

A ∩ B = {c∈U; c∈A a c∈B}.

Pokud je průnik dvou množin prázdný, řekneme, že jsou disjunktní.

Jestliže mají množiny A a B konečně mnoho prvků, pak máme následující zajímavý vzorec pro velikost jejich sjednocení (zkuste se nad tím zamyslet, vyplyne to už selským rozumem):

|A ∪ B| = |A| + |B| − |A ∩ B|.

Rozdíl. Jsou-li dány množiny A a B ve vesmíru U, definujeme jejich rozdíl jako

A − B = {c∈U; c∈A a c∉B}.

Všimněte si, že to má smysl, nejen když je B podmnožinou A, ale i obecně. Intuitivně vzato si množina B "ukousne" z A, takže části B mimo A neudělají nic. V extrémním případě, pokud jsou B a A disjunktní, rozdíl A − B dává A.

Symetrický rozdíl. Jsou-li dány množiny A a B ve vesmíru U, definujeme jejich symetrický rozdíl jako

A÷B = {c∈U; c∈A a c∉B nebo c∈B a c∉A}.

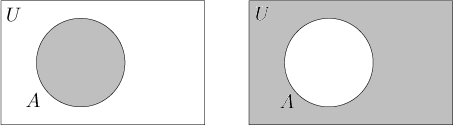
Při práci s množinami nám pomáhají Vennovy diagramy. Tradiční Vennovy diagramy jsou kruhy, které představují množiny, umístěné uvnitř obdélníka představujícího vesmír. V zásadě máme dva druhy diagramů. Někdy pomocí nich ukazujeme nějakou konkrétní situaci. Například na následujícím obrázku je nalevo množina A a napravo ukážeme její doplněk A^c.

Na následujícím obrázku ukazujeme situaci, kdy je B podmnožinou A.

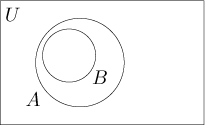
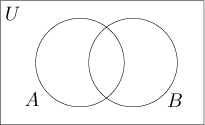
Častěji ale pomocí diagramů přemýšlíme nad různými problémy. Pak potřebujeme, aby obrázek zachytil situaci obecně; jinými slovy, na obrázku pak musí být místa k zachycení všech možných prvků vzhledem k množinám. Pokud máme dvě množiny, pak tam musí být místa pro prvky, které jsou v obou množinách, pak pro prvky, které jsou jen v jedné množině, a také pro prvky, které nejsou v ani jedné množině.

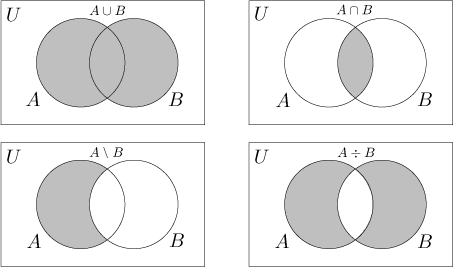
Na následujícím obrázku ukazujeme operace, které jsme předtím probrali.

Pro tři množiny potřebujeme jiný obrázek.

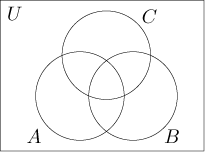
Není možné nakreslit tradiční Vennův diagram pro čtyři množiny. Ať už uspořádáme čtyři kruhy jakkoliv, vždy budou prvky, které do obrázku nezakreslíme. Pokud například zkusíme tento obrázek,

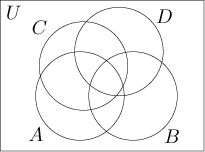
pak nemůžeme nakreslit body, které leží v A a D, ale nejsou v B ani v C.

Pokud nahradíme kruhy obdélníky, pak se čtyři množiny dají udělat, navíc jako bonus vypadají diagramy moderněji. Čtvrtý obrázek ukazuje modifikaci obrázku pro čtyři množiny, podobně lze modifikovat i obrázek se třemi množinami.

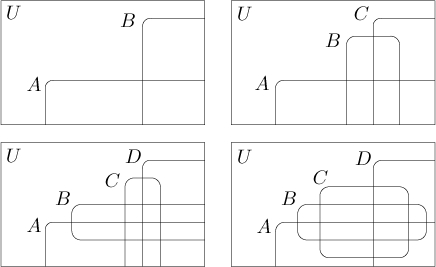
Lidé se snažili najít způsob, jak zobrazit více množin, jako příklad ukážeme Edwardsovy diagramy pro tři až šest množin.

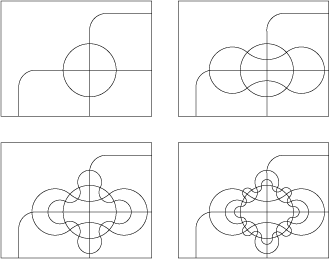
Ve Vennově diagramu můžeme označit prvky množiny. Množinu A = {1,2,3} můžeme nakreslit takto:

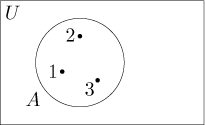
Pokud je množina uspořádaná, používáme také tento obrázek:

Takový typ obrázku často používáme pro číselné množiny, například celá čísla.

Uvažujme množiny A a B. Jejich kartézský součin definujeme jako množinu

A×B = {(a,b); a∈A a b∈B}.

Příklad: Uvažujme množiny A = {a,b,c} a B = {1,2}. Pak

A×B = {(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)}.

Kartézský součin kreslíme takto:

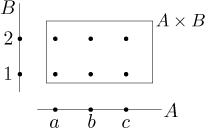
Například pravá horní tečka znázorňuje pár (c,2).

Zobrazení
Zpět na Extra - Množiny a zobrazení