Zobrazení, kardinalita

Zde uvedeme zobrazení, podíváme se na jejich vlastnosti a zavedeme operace. Na konci sekce se podíváme na porovnání velikostí množin.

Definice.
Uvažujme množiny A a B. Definujeme transformaci či zobrazení z A do B jako libovolnou podmnožinu T kartézského součinu A×B splňující následující podmínku:

Pro každé a z A existuje právě jedno b z B takové, že (a,b)∈T.

Píšeme T : A ↦ B.

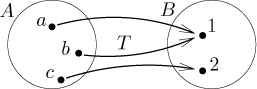
Příklad: Uvažujme množiny A = {a,b,c} a B = {1,2}. Pak třeba

T = {(a,1),(b,1),(c,2)}

je zobrazení z A do B.

Zobrazení si představujeme jako černou skříňku, která posílá prvky jedné množiny do jiné množiny, například prvek a je poslán do 1. Podmínka v definici v zásadě říká, že prvek z A nemůže být poslán na dvě (či více) různých míst v B. Na druhou stranu ale není problém poslat dva různé prvky na stejné místo, jak ostatně v tom příkladu vidíme. Poznamenejme, že v zobrazení neusíme využít všech prvků B.

Tato představa posílání ze odráží i ve speciálním značení, které pro zobrazení používáme. Namísto abychom říkali že řekněme (a,1) je v T, píšeme T (a) = 1. Říkáme, že 1 je obraz prvku a v zobrazení T nebo že 1 je hodnota zobrazení T v a. Někdy také používáme značení

T : a ↦ T(a).

Výchozí množině A říkáme definiční obor T, značíme D(T ). Alternativní značení: D_T nebo dom(T ). Cílová množina B je jako taková méně zajímavá než definiční obor, už proto, že může obsahovat prvky navíc, které s daným zobrazením nesouvisí. Zajímavější je obor hodnot T, což je množina všech prvků B, které jsou obrazy nějakých prvků A v zobrazení T. Značíme jej R(T ), alternativy jsou R_T, H(T ), nebo ran(T ). V našem příkladě máme D(T ) = A a R(T ) = B, to druhé se tak často nestává.

Když umíme posílat prvky, umíme také posílat množiny. Je-li D podmnožina A, pak obrazem D v zobrazení T je množina

T [D] = {T(d); d∈D}.

Například R(T ) = T [A].

Poznámka. Někteří autoři také používají název funkce jako ekvivalent zobrazení. Jiní autoři si ale tento název rezervují pouze pro zobrazení, která pracují s čísly, zatímco slovo zobrazení či transformace naznačuje obecnější situaci. Tento přístup jsme zde přijali také, ale protože nejde o všeobecně uznávanou konvenci, nebudeme se po tom moc vozit.

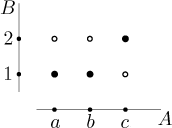
Existují dva populární způsoby, jak kreslit zobrazení. Jeden je graf T, kdy nějak zvýrazníme, které prvky kartézského součinu A×B se vyskytují v T. Například ten příklad výše je možné zaznačit takto:

V praxi se obvykle nezdržujeme kreslením nepoužitých prvků toho součinu a použijeme raději tento obrázek.

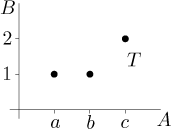
Kreslení takového grafu je asi nejpopulárnější vizualizací zobrazení, ale někdy o zobrazení více vypovídá jiný druh obrázku a je tedy užitečnější.

Pro uspořádané množiny (obzvláště číselné množiny) zase často dáváme přednost jinému obrázku.

Než se posuneme dále, uvedeme zobrazení, které je definováno vždy, když máme množinu.

Definice.
Uvažujme množinu A. Definujeme identitu na A, značíme Id_A, jako zobrazení z A do A definované vzorcem Id_A(a) = a pro všechna a z A.

Zobrazení mají dvě důležité vlastnosti.

Definice.
Uvažujme zobrazení T z A do B.
Řekneme, že T je prosté či injektivní nebo že je to injekce, jestliže pro každé dva různé prvky a₁, a₂ z A se nerovnají také jejich obrazy T(a₁), T(a₂).

Řekneme, že T je na či surjektiví nebo že je to surjekce, jestliže R(T ) = B. Říkáme, že T je zobrazení "z A na B".

Podmínka pro injektivitu říká, že není možné poslat dva různé prvky na stejné místo. Zde máme výhodu, že se nesnažíme předstírat formální dokonalost, takže jsme to takto mohli říct. Pokud bychom chtěli definici zapsat správně formálně, byla by trochu komplikovanější než následující alternativní definice. Zobrazení je prosté, pokud platí následující podmínka: Jestliže jsou dva prvky poslány na stejné místo, pak se musely už od začátku rovnat.

T(a₁) = T(a₂) ↦ a₁ = a₂.

Pro matematika je tento výrok mnohem hezčí, proto se často používá. Je také výhodnější pro praktické používání, protože práce s relací "nerovná se" může být zákeřná, zatímco s nerovnostmi pracovat umíme.

Příklady: Na následujícím obrázku jsou dvě zobrazení v prvním řádku prostá, zatímco zobrazení ve druhých dvou řádcích prostá nejsou.

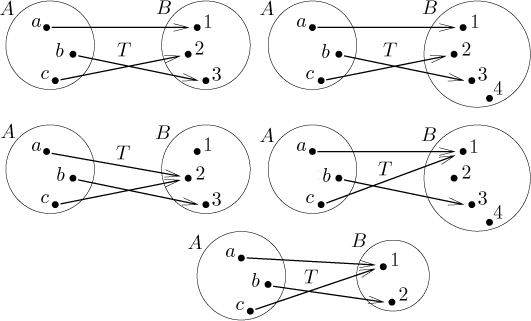
Teď surjektivitu, ty dva příklady v prvním řádku jsou na, zatímco ostatní ve druhých dvou řádcích na nejsou.

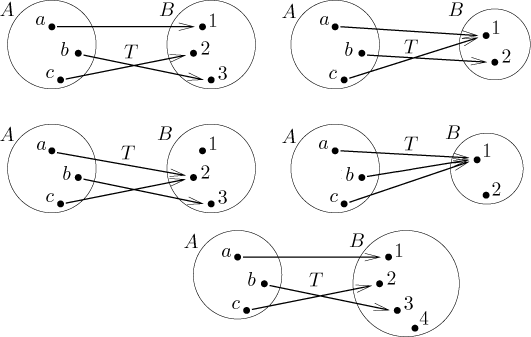
Všimněte si, že někdy jsou tyto vlastnosti již určeny počtem prvků v oněch dvou množinách. Na obrázku o prostotě si v úplně posledním příkladě všimněte, že nemáme šanci vytvořit prosté zobrazení z A do B, prostě proto, že v cílové množině nemáme dostatek prvků. Podobně v obrázku o surjektivitě není u posledního příkladu šance udělat zobrazení na B, protože se nelze dostat ke čtyřem prvkům jen třemi šipkami.Obecně vzato, pokud jsou A a B konečné množiny a velikost A je větší (ostře) než velikost B, pak nelze udělat prosté zobrazení z A do B; na druhou stranu není šance na surjektivitu, pokud je velikost A (ostře) menší než velikost B. Můžeme také přejít k ekvivalentním výrokům: Pokud existuje nějaké prosté zobrazení z A do B, pak B musí mít alespoň tolik prvků, kolik má A. Pokud existuje prosté zobrazení z A na B, pak A musí mít alespoň tolik prvků, kolik má B.

Ony dvě vlastnosti se spojí ve velice užitečný pojem.

Definice.
Uvažujme zobrazení T z A do B.
Řekneme, že T je vzájemně jednoznačné nebo že to je bijekce, jestliže je prosté a na.

Mezi všemi předchozími příklady je jen jedna bijekce, jmenovitě horní levý příklad v posledním (a předposledním) obrázku. Bijekce jsou velice užitečné, protože nám umožňují porovnávat množiny. Například z poznámky o velikostech množin před chvílí můžeme odhadnout, že když máme dvě konečné množiny, tak je nelze spojit bijekcí, pokud nemají stejný počet prvků; naopak pokud nějaká bijekce existuje, pak ty dvě množiny musí mít stejný počet prvků. Na tohle se podíváme blíže v poslední části této sekce.

Intuitivně, jestliže máme dvě množiny a bijekci mezi nimi, pak máme páry z prvků těchto množin. Potom se zdá, že směr šipek již není podstatný. To je pravda, na tohle se podíváme v následující části.

Začneme něčím velice jednoduchým, vlastně se to mezi operace nepočítá, ale je to něco, co můžeme dělat se zobrazeními.

Definice.
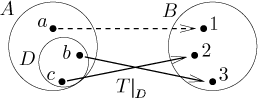
Uvažujme zobrazení T z A do B. Nechť D je podmnožina A. Definujeme restrikci T na D jako zobrazení S z D do B definované předpisem S(d) = T(d) pro všechna d z D.

Lidově řečeno, prostě předpokládáme, že T mimo D neexistuje, a dostaneme restrikci. Značíme ji T |_D.

Protože zde pracujeme s obecnými množinami, nejsou žádné operace (jako sčítání apod.) k dispozici. Jediná věc, kterou tedy můžeme obecně zkusit, je podívat se na skládání zobrazení.

Definice.
Nechť T je zobrazení z A do B a nechť S je zobrazení z B do C. Pojmem složení nebo kompozice těchto dvou zobrazení míníme zobrazení S ○ T z A do C definované předpisem

S ○ T : a ↦ S(T(a)) pro a z A.

Takže nejprve najdeme obraz a pomocí T a pak tento obraz dosadíme do S. Obrázek ukazuje, že to má smysl, protože obrazy pomocí T jsou přesně tam, kde funguje S; přesně řečeno, obor hodnot T je podmnožinou definičního oboru S.

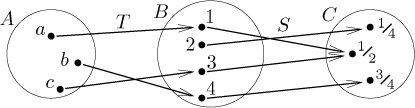
Například (S ○ T )(a) = S(T(a)) = ½. V principu tedy "vynecháme prostředníka", skládání znamená, že je každý prvek z A poslán dvakrát za sebou a pak předstíráme, že jde jen o jedno poslání, čímž dostaneme nové zobrazení.

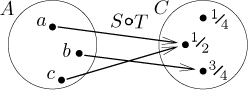
Všimněte si, že se značení pro skládání čte "zprava doleva", tj. při dosazování nejprve použijeme funkci napravo a pak teprve funkci nalevo. To může být zpočátku nezvyklé a začátečníci to občas popletou, ale má to smysl, protože toto pořadí je stejné jako u alternativního značení S(T ). Všimněte si také, že když máme množiny a zobrazení jako na posledním obrázku, tak nelze skládat v opačném pořadí. Skládání T ○ S = T(S ) nelze uskutečnit: Pokud dosadíme prvek z B do S, tak dostaneme prvek z C, ale T na C nepracuje.

Všimněte si dále, že v takovém složeném zobrazení záleží na tom druhém zobrazení S jen tam, kam se lze dostat pomocí T; jinými slovy, hodnoty S v prvcích B, které nejsou částí R(T ), jsou pro složené zobrazení irelevantní. Pomocí tohoto pozorování dostaneme snadno následující tvrzení, která spojují vlastnosti a skládání:

Fakt.
Nechť T je zobrazení z A do B a nechť S je zobrazení z B do C.
Jestliže jsou T i S prostá, pak je S ○ T také prosté.
Jestliže T není prosté, tak také S ○ T není prosté.

Jestliže jsou T i S na, pak je také S ○ T na.
Jestliže S není na, pak také S ○ T není na.

Jestliže jsou T i S bijekce, pak je také S ○ T bijekce.

Je docela zajímavé si rozmyslet některé implikace, které se nabízí, ale nejsou zde vypsány, evidentně proto, že neplatí. Například následující obrázek ukazuje, že se může stát, že S není prosté, ale složení už je.

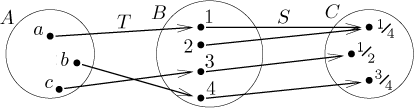
Na druhou stranu na předchozím obrázku S prosté nebylo a kompozice také ne. To ukazuje, že pokud prostota selže u S, tak prostota složení then the injectivity of the composition S ○ T záleží na tom, jakým způsobem ta prostota u S selhala. Podobné pozorování funguje i pro surjektivitu. Zkuste si vymyslet příklad, kde T není na, ale složení už je; nebo příklad, kde T ani S nejsou bijekce, ale S ○ T je. Mimochodem, z předchozích tvrzení také vyplává, že pokud složíme dvě zobrazení a jedno je bijekce, pak se vlastnosti toho dtuhého (prostota, surjektivita) zachovají.

Když už máme skládání, můžeme přejít k další důležité definici.

Definice.
Nechť T je zobrazení z A do B. Řekneme, že zobrazení S z B do A je inverzní zobrazení k T, značeno T ⁻¹, jestliže

S(T(a)) = a pro každé a z A   a
T(S(b)) = b pro každé b z B.

Pokud takové inverzní zobrazení existuje, then pak řekneme, že T je invertibilní.

Lidově řečeno, tato dvě zobrazení si navzájem ruší svůj účinek. Jestliže T někam pošle a, pak to S pošle zpět, a naopak.

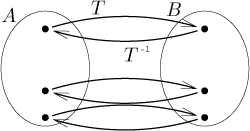
Symetrie v tomto obrázku znamená, že býti inverzí je v jistém smyslu symetrický pojem, tedy také platí, že T je inverzní k T ⁻¹, což se dá zapsat takto: (T ⁻¹)⁻¹ = T. Pokud takové inverzní zobrazení existuje, pak je jednoznačné.
Všimněte si, že D( T ⁻¹) = R( T ) a R( T ⁻¹) = D( T ).

Předtím jsme měli spoustu obrázků s příklady zobrazení, které byly či nebyly prosté/na. Pokud nad nimi chvíli přemýšlíte, měli byste začít mít dojem, že není možné "obrátit" akci zobrazení, které není prosté či na. V prvním případě jdou dvě šipky do stejného místa, takže evidentně není možné udělat šipku "opačně" pro inverzní zobrazení a první rovnost v definici není splněna. Pokud T není na, pak existuje prvek v B, který není cílem žádné šipky, takže zase není možné udělat "opačnou" šipku, tentokráte nefunguje ta druhá podmínka z definice.

Věta.
Nechť T je zobrazení z A do B. Je invertibilní tehdy a jen tehdy, když je to bijekce.

Poznámka: Jestliže je zobrazení bijekce, pak je invertibilní, podle předchozí poznámky je také inverzní zobrazení invertibilní a tudíž je toto inverzní zobrazení také bijekce.

Je zajímavé spojit pojem inverzní funkce se skládáním. Podmínku v definici inverzní funkce je možné přepsat takto:

T ⁻¹ ○ T = Id_A     a     T ○ T ⁻¹ = Id_B.

To naznačuje zajímavou strukturu pro operaci skládání. Pokud jste zvědaví, podívejte se na tuto poznámku.

Všimněte si, že jestliže zobrazení z A do B není na, pak v B zůstanou nevyužité prvky. V mnohých případech je můžeme ignorovat, dostaneme tak následující tvrzení.

Věta.
Nechť T je zobrazení z A do B. Pokud jej budeme uvažovat za zobrazení z A do R(T ), pak je to bijekce (a tedy je invertibilní) tehdy a jen tehdy, je-li prosté. Pak také má inverzi T ⁻¹ z R(T ) do A.

Pokud jsou dvě množiny konečné, můžeme porovnat jejich velikosti tak, že prostě spočítáme počet prvků v každé z nich. Jak už jsme viděli před chvílí, rovnost velikostí lze také určit tak, že si položíme následující otázku: Existuje bijekce z jedné množiny na druhou? Tento druhý způsob je použit jako definice, protože pracuje nejen pro konečné, ale i pro nekonečné množiny. Pak ale nemluvíme o velikosti, ale o kardinalitě.

Definice.
Uvažujme dvě množiny A a B. Řekneme, že mají stejnou kardinalitu, značeno |A| = |B|, jestliže existuje bijekce z A na B.

Řekneme, že kardinalita A je menší nebo rovna kardinalitě B, značeno |A| ≤ |B|, jestliže existuje prosté zobrazení z A do B.

Ekvivalentně, |A| ≤ |B| jestliže existuje zobrazení z B na A. Toto srovnání se chová velice rozumně, například každá množina A splňuje |A| ≤ |A| a |A| = |A|, snadno se také ukáže, že tato relace je tranzitivní (viz Uspořádání v příští sekci). Dá se také ukázat, že libovolné dvě množiny lze porovnat, jinými slovy pro libovolné dvě množiny A, B platí |A| ≤ |B| nebo |B| ≤ |A|.

Pocit "normálnosti" potvrdí tvrzení zvané Cantor-Bernsteinova věta: Jestliže |A| ≤ |B| a |B| ≤ |A|, pak nutně |A| = |B|. To zní jako něco jasného, ale protože porovnávání velikosti množin funguje přes existenci zobrazení, tak je ve skutečnosti docela obtížné ukázat, že věci fungují, jak bychom chtěli. Můžeme také definovat ostré porovnání, |A| < |B| jestliže |A| ≤ |B|, ale neplatí |A| = |B|. I tato relace funguje tak, jak by jeden čekal.

Řekneme, že množina A je konečná, jestliže je buď prázdná (pak má kardinalitu nula) nebo existuje přirozené číslo n takové, že A má stejnou kardinalitu jako množina {1,2,...,n}, v kterémžto případě řekneme, že A má kardinalitu n. Značíme to |A| = n, někdy také #A = n. Jinak řekneme, že je tato množina nekonečná, někdy lidé píší |A| = ∞.

Jak už jsme viděli, pro konečné množiny pojem kardinality souhlasí s intuitivním pojmem velikosti. Pro nekonečné množiny je to mnohem zajímavější, protože se ukáže, že existuje mnoho "velikostí" nekonečna. Jedna z nejdůležitějších "velikostí" je kardinalita množiny přirozených čísel (viz následující sekce).

Definice.
Uvažujme množinu A. Řekneme, že tato množina je spočetná, jestliže má stejnou kardinalitu jako množina ℕ všech přirozených čísel.

Spočetné množiny jsou ty, jejichž prvky lze "očíslovat" či "oindexovat". Uvažujme spočetnou množinu A. Podle definice musí existovat nějaká bijekce T z A na množinu ℕ. Teď tedy můžeme seřadit prvky A podle čísla, které je jim přiřazeno skrz T. Nejprve vezmeme prvek a takový, že T(a) = 1, budeme mu říkat a₁, pak vezmeme prvek a takový, že T(a) = 2, můžeme mu říkat a₂, a tak dále, a protože T přiřazuje číslo ("index") každému prvku A, tak nakonec tímto způsobem dostaneme celou množinu A.

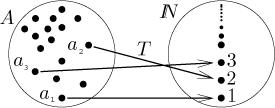
Tato vlastnost "očíslovatelnosti" je velice užitečná, proto spočetné množiny vítáme, už proto, že takovéto množiny lze vyčerpat indukcí. Mimochodem, spočetnost je nejmenší velikost nekonečných množin. Jaké množiny jsou spočetné? Ukáže se, že jich je docela dost, protože "spočetná" velikost nekonečna toho hodně snese. Začneme jednoduchým pozorováním, že přidáním jednoho prvku do spočetné množiny nezměníme její velikost. Abychom to dokázali, stačí ukázat, že množina přirozených čísel má stejnou kardinalitu jako množina přirozených čísel obohacená o 0. Použijeme bijekci T(n) = n − 1, rozmyslete si, že je opravdu prostá a na. Obrázek ukazuje, že intuitivně lze opravdu spárovat prvky těchto dvou množin (šipky odpovídají našemu T ) a tedy mají stejnou "velikost".

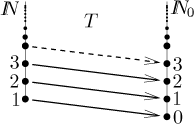
Vidíme, že přidáním jednoho prvku k nekonečné množině nezměníme její velikost. Můžeme ale říct víc. Pokud zvětšíme spočetnou množinu přidáním stejně velké množiny, pořád bude spočetná. Jeden způsob, jak toto ukázat, je dokázat, že

množina celých čísel je spočetná,

protože víme, že vzniknou tak, že vezmeme přirozená čísla a přidáme přirozená čísla se znaménky mínus (viz další sekce). Intuitivně bychom řekli, že celých čísel je dvakrát víc než přirozených, ale nekonečna jsou zrádná.

Nejprve si musíme v přirozených číslech vyrobit nekonečně mnoho děr, aby bylo místo na záporná celá čísla. Uvažujme zobrazení T(n) = 2n z množiny ℕ do ℕ.

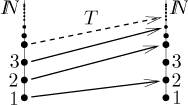
Toto vlastně ukazuje, že množina přirozených čísel má stejnou velikost jako množina sudých přirozených čísel, ale pro nás jsou teď důležité ty díry napravo. Je jich evidentně nekonečně mnoho, takže nabízí místa, kam poslat záporná čísla.

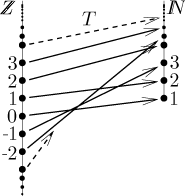
Toto konkrétní T je definováno takto: T(n) = 2n pro kladná celá čísla a T(n) = 1 − 2n pro nulu a záporná celá čísla. Snadno se ověří, že je to bijekce z množiny celých čísel na přirozená čísla. Už jsme zmínili, že spočetnost je ekvivalentní schopnosti očíslovat danou množinu. Spočetnost celých čísel lze také vyargumentovat tak, že nalezneme způsob, jak očíslovat všechna celá čísla, například takto:

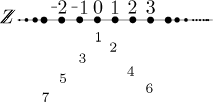
Číslujeme tak, že stále skáčeme zleva doprava, evidentně tak nakonec tímto způsobem očíslujeme všechna celá čísla. Mimochodem, toto číslování přesně odpovídá té použité bijekci. Tuto alternativní úvahu jsme zde uvedli, protože ji použijeme k důkazu následujícího a nejtroufalejšího tvrzení: Pokud k přirozeným číslům přidáme nekonečně mnoho kopií této množiny, pak zase dostaneme spočetnou množinu. Jinými slovy, kartézský součin přirozených čísel s přirozenými čísly má stejnou velikost jako původní množina. Dokážeme to tak, že najdeme způsob, jak očíslovat všechny páry. Nejprve naznačíme číslování prvních několika párů a pak ukážeme obecnou metodu.

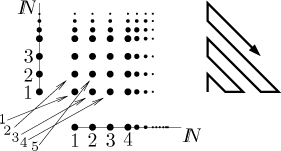
Zdá se jasné, že pokud následujete naznačený vzor, pak nakonec očíslujete všechny páry. Teď se na tento výsledek podíváme ze dvou úhlů pohledu. Za prvé, pokud se díváme na spočetné nekonečno jako na nějaký abstraktní objekt, pak ten první fakt o spočetnosti říká, že vlastně ∞ + 1 = ∞. Indukcí vidíme, že přičtení přirozeného čísla nekonečno nezmění. Druhý fakt (celá čísla jsou spočetná) říká (z tohoto úhlu pohledu), že ∞ + ∞ = ∞, ale také že 2 ⋅ ∞ = ∞. Indukcí se dá ukázat, že vlastně n ⋅ ∞ = ∞ pro libovolné přirozené číslo n. No a (zatím) poslední fakt (o kartézském součinu) říká, že také ∞ ⋅ ∞ = ∞, tj. ∞² = ∞. A zase indukcí ∞ⁿ = ∞ pro každé přirozené číslo n. Zde se to ale zastaví, protože ∞^∞ je mnohem větší než to původní nekonečno, dokonce už 2^∞ je větší. Nebudeme do toho hlouběji vrtat, místo toho se ještě vrátíme k poslednímu faktu.

Tvrdíme, že

množina racionálních čísel je spočetná.

Za prvé, protože racionální čísla obsahují přirozená čísla, tak je jasné, že jsou také nejméně spočetné. Těžší částí je tedy dokázat, že jsou také nejvýše spočetné. Připomeňme, že jsme dokázali, že množina všech párů (a,b) přirozených čísel je spočetná. Protože víme, že zdvojnásobení nemění velikost nekonečných množin, vyplývá odtud, že také množina

M = {(a,b); a celé číslo, b přirozené číslo}

je spočetná. Zobrazení S definované vzorcem S(a,b) = a/b je zobrazení z M na racionální čísla, což znamená, že velikost racionálních čísel je nejvýše taková, jako velikost M, tedy racionální čísla jsou nejvýše spočetná. Důkaz je hotov.

Vidíme tedy, že všechny množiny, které jsme dostali při pokusu vyřešit nějaké algebraické zádrhele (viz následující sekce) jsou spočetné. To ale není pravda o reálných číslech.

Množina reálných čísel není spočetná.

Klasický důkaz tohoto tvrzení ukazuje, že ať už se reálná čísla pokusíte očíslovat jakkoliv, vždycky nějaké zbyde. Je překvapivě jednoduchý, ale pořád příliš dlouhý na tuto sekci; musíte nám tedy věřit. Protože spojením dvou spočetných množin získáme zase spočetnou množinu a racionální čísla jsou spočetná, vyplývá z toho, že máme nespočetně mnoho iracionálních čísel. Jinými slovy, když se v rovině podíváme na přímku, vybereme si nějaký bod jako počátek a pak zaznačíme všechny body, jejichž vzdálenost od počátku je racionální, pak na této přímce dostaneme podstatně více děr než teček.

Kardinalita množin byla důkladně studována už docela dlouho, jsou množiny, které jsou dokonce větší než množina reálných čísel a dokonce ještě větší atd. (existuje nekonečný řetězec nekonečných velikostí), ale jedna zdánlivě jednoduchá otázka je stále otevřená: Je kardinalita reálných čísel hned ta po spočetnosti, nebo je množina, jejíž kardinalita by byla striktně větší než spočetnost ale striktně menší než kardinalita reálných čísel? Většina matematiků si myslí, že žádná přechodná velikost neexistuje, říká se tomu Hypotéza kontinua, ale nikdo to zatím neuměl dokázat. Pokud náhodou máte nějaký nápad, máte dobrou šanci na nějakou významnou matematickou cenu.

Důležité číselné množiny
Zpět na Extra - Množiny a zobrazení