Definice.
Nechť f je funkce definovaná na nějakém okolí bodu
![]() ∈ℝn.
∈ℝn.
Řekneme, že f má v ![]() lokální maximum nebo že
lokální maximum nebo že
![]() )
)![]() )
)![]() ) ≥ f (
) ≥ f (![]() )
)![]() ∈U.
∈U.
Řekneme, že f má v ![]() lokální minimum nebo že
lokální minimum nebo že
![]() )
)![]() )
)![]() ) ≤ f (
) ≤ f (![]() )
)![]() ∈U.
∈U.
Definice lokálního extrému se zcela přirozeně přenese do více rozměrů.
Definice.
Nechť f je funkce definovaná na nějakém okolí bodu∈ℝn.
Řekneme, že f má v
lokální maximum nebo že
f ( je lokální maximum, jestliže existuje okolí)
U = U( takové, že)
f ( pro všechna) ≥ f (
)
∈U.
Řekneme, že f má v
lokální minimum nebo že
f ( je lokální minimum, jestliže existuje okolí)
U = U( takové, že)
f ( pro všechna) ≤ f (
)
∈U.
Obrázek níže pro případ dvou proměnných ukazuje vlevo dvě lokální maxima a vpravo jedno lokální minimum.
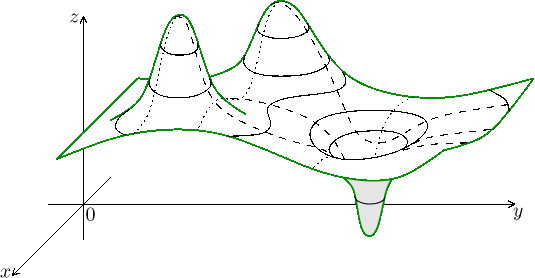
Podobně si to představujeme ve více dimenzích. Lokální maximum má vlastnost, že když skrze něj řízneme graf v libovolném směru (čímž se z toho stane situace funkce jedné proměnné), tak tam pořád máme lokální maximum v klasickém významu. Obdobná vlastnost platí pro lokální minimum.
Ve více dimenzích existuje ještě jeden zajímavý typ chování, který na obrázku vidíme mezi oněmi dvěma kopci. Pokud tam graf řízneme svislou rovinou ve směru vedoucím mezi vrcholy, pak v tom údolíčku mezi nimi vidíme na řezu lokální minimum. Když ale řízneme graf ve směru kolmém, tak v tom údolí uvidíme na řezu lokální maximum. Takovýmto bodům říkáme sedlo či sedlový bod a při zkoumání extrémů se také připlétají do hry, takže se běžně berou jako součást zkoumání extrémů.
Jak lokální extrémy najdeme? Postup je obdobný vyšetřování lokálních extrémů pro funkce jedné proměnné. Zhruba řečeno, nejprve najdeme kandidáty pomocí první derivace, pak je posoudíme pomocí druhé.
Když graf řízneme libovolnou svislou rovinou skrz nějaký lokální extrém
![]() ,
bude extrém i na řezu, tedy derivace
v
,
bude extrém i na řezu, tedy derivace
v ![]() v tomto směru musí být nulová. Jestliže
mají být všechny směrové derivace nulové, pak musí být nulový (jako vektor)
i gradient v
v tomto směru musí být nulová. Jestliže
mají být všechny směrové derivace nulové, pak musí být nulový (jako vektor)
i gradient v ![]() .
.
Jiná úvaha: V lokálním extrému je tečná nadrovina vodorovná, musí tedy mít normálový vektor svislý. Jak jsme se dozvěděli v předchozí části, jako normálový vektor je moné vzít
![]()
Tento vektor je svislý, pokud
![]() (
(![]() ) = 0
) = 0![]() ) =
) = ![]() .
.
Věta.
Nechť f je funkce definovaná na nějakém okolí boduJestliže má f v ∈ℝn.
lokální extrém a gradient tam existuje, pak
∇ f ( ) =
.
Bodům, kde
![]() ) =
) = ![]() ,
,![]() (
(![]() ) = 0
) = 0
Jako obvykle neplatí naopak, že stacionární body dávají lokální extrémy. Například typický sedlový bod u funkce dvou proměnných je také stacionární bod. Když tedy najdeme stacionární body, je potřeba je ještě klasifikovat. K tomu slouží Sylvestrovo kritérium. Je mnohem snažší si jej pamatovat, pokud si umíme představit, co se děje.
Lokální maximum se pozná podle toho, že je maximem ve všech řezech, mimo
jiné i v řezech rovnoběžných s osami. V situaci jedné proměnné ovšem maximum
poznáme snadno podle druhé derivace, takže ve více dimenzích u lokálního
maxima očekáváme
![]() (
(![]() ) < 0
) < 0![]() (
(![]() ) > 0
) > 0
Podívejme se na případ dvou proměnných. Extrém (tedy maximum i minimum) mají
společné to, že jsou znaménka
![]() (x, y)
(x, y)![]() (x, y)
(x, y)![]() (x, y)⋅
(x, y)⋅![]() (x, y) > 0.
(x, y) > 0.![]() (x, y)⋅
(x, y)⋅![]() (x, y) < 0,
(x, y) < 0,
Vidíme, že by součin nesmíšených druhých derivací mohl sloužit jako prvotní
ukazatel, zda máme extrém nebo sedlo. Pokud vyjde, že je extrém, tak se k
rozlišení maxima a minima stačí podívat na nějaký řez, tedy stačí uvažovat
znaménko libovolné nesmíšené druhé derivace, třeba
![]() (x, y).
(x, y).
Tyto úvahy nejsou zcela špatně, je tu ovšem nepříjemná mezera. Viděli jsme, že extrémy vedou na kladné znaménko součinu těch dvou derivací, ale my bychom potřebovali opačný směr. Jestliže zjistíme, že znaménko toho součinu je kladné, znamená to, že máme lokální extrém? Bohužel ne.
Problém je v tom, že je třeba také vzít v úvahu vliv derivace smíšené, tedy musíme uvažovat souhru složek Hessovy matice
![]()
První rozhodnutí mezi extrémem a sedlem jsme před chvílí dělali pomocí
součinu hlavní diagonály této matice, což čtenáři doufejme připomnělo
determinant. Ukáže se, že to opravdu takto funguje,
1. Řešením rovnice
![]()
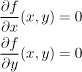
najdeme stacionární body ![]() .
.
2. Pro každý stacionární bod najdeme odpovídající Hessovu matici
![]() ).
).
3. Jestliže ![]() sedlový bod.
sedlový bod.
4. Jestliže ![]() lokální extrém.
Je to lokální maximum pokud
lokální extrém.
Je to lokální maximum pokud
![]() (
(![]() ) < 0,
) < 0,![]() (
(![]() ) > 0.
) > 0.
V případech, kdy vychází v klíčových okamžicích nuly, rozhodovací algoritmus selhává, nic nevíme a je třeba použít pokročilejší metody, které jsou za rámec tohoto úvodu.
Pokud budeme chtít tento proces zobecnit pro více proměnných, musíme se na
něj podívat trochu z jiné strany. Nejprve si všimneme, že ve čtvrtém kroku
vlastně také zkoumáme znaménko matice, jmenovitě podmatice H dané
levým horním rohem. To je zajímavá inspirace, představíme si rozsáhlou
matici H a zeptáme se, co lze čekat od znamének levých horních
subdeterminantů, které se tradičně značí
Připomeňme, že u lokálního maxima očekáváme
![]() (
(![]() ) < 0
) < 0![]() (
(![]() ) > 0
) > 0
První subdeterminant je dán levým horním rohem H, tedy
![]()
Pro maximum vychází záporný, pro minimum kladný.
Druhý subdeterminant je dán maticí
![]()
Pro maximum vychází kladný, pro minimum také kladný.
Třetí subdeterminant je dán maticí
![]()
Pro maximum vychází záporný, pro minimum kladný.
Čtenář si jistě hravě domyslí, jak to funguje dál. Pro maxima se znaménka stále střídají, pro minima jsou všechny detetminanty kladné.
Pokud nastane jiná konstelace znamének, pak maximum ani minimum nenastává,
pokud někde vyskočí nuly, pak tento rozhodovací proces neuspěl a nevíme, co
se v ![]() děje.
děje.
To, co jsme právě odvodili pro případ diagonální H, platí i obecně.
Věta (Sylvestrovo kritérium).
Nechť f je definováno a má spojité derivace druhého řádu na nějakém okolí bodu, který je pro f stacionární, tedy
∇ f ( Nechť H je Hessova matice f v) = 0.
, nechť
Δi jsou její levé horní subdeterminanty.Jestliže
Δi > 0 pro všechna i, pak jef ( lokální minimum.)
Jestliže
Δ1 < 0, Δ2 > 0, Δ3 < 0 atd. až(−1) nΔn > 0, pak jef ( lokální maximum.)
1. Řešením rovnice
![]() ) =
) = ![]()
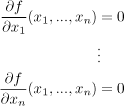
najdeme stacionární body ![]() .
.
2. Pro každý stacionární bod najdeme odpovídající Hessovu matici
![]() ).
).
3. Spočítáme subdeterminanty
4. Pokud
![]() lokální minimum.
lokální minimum.
Pokud se znaménka střídají
![]() lokální maximum.
lokální maximum.
Příklad.
Najdeme a klasifikujeme lokální extrémy funkce
Nejprve najdeme stacionární body. Rovnice
![]() ) =
) = ![]()
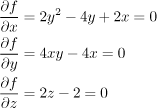
Je to soustava tří rovnic o třech neznámých, to zní nadějně, ale rovnice nejsou lineární, tudíž celá ta krásná teorie nepomůže. Jak řešíme obecné soustavy?
My si hned všimneme, že třetí rovnice je nezávislá, tudíž jistě
Zaměříme se na druhou rovnici, kterou si přepíšeme do tvaru
V případě
V případě
Teď je třeba všechny tři stacionární body prozkoumat, tedy potřebujeme Hessovu matici. Připravíme si druhé parciální derivace, díky symetrii u smíšených stačí šest:
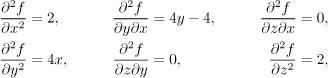
Hessova matice je
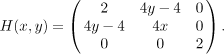
A jdeme na to:
Bod
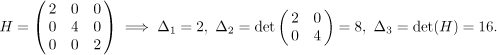
Znaménka jsou postupně +, +, +, proto je
Bod
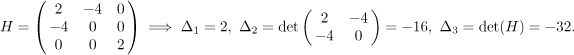
Znaménka jsou postupně +, -, -, proto
Bod
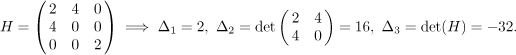
Znaménka jsou postupně +, +, -, proto
Příklad.
Najdeme a klasifikujeme lokální extrémy funkce
Nejprve najdeme stacionární body. Řešíme rovnice
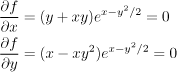
Exponenciála je vždy kladná, mohou se jí rovnice vydělit a stačí řešit
rovnice
Jestliže
Jestliže
Připravíme si druhé parciální derivace:
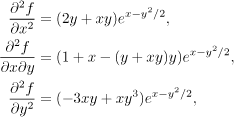
Hessova matice je
![]()
![]()
Protože jde o funkci dvou proměnných, použijeme první algoritmus, kdy
nejprve posoudíme
Bod
![]()
tedy
Bod
![]()
tedy
Bod
![]()
tedy
Funkce více proměnných: Integrál
Zpět na Extra - Funkce více proměnných