Příklad: Dokažte, že pro všechna čísla t ≥ 0 máme

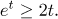
Řešení: Označme f (t) = e^t a g(t) = 2t. Potřebujeme dokázat, že f ≥ g na intervalu I = ⟨0,∞). Protože to nevypadá, že by pomohly algerbaické postupy, tkusíme teoretický přístup, jmenovitě pomocí derivace, jak je popsáno například v části zde v části Přehled metod - Věta o střední hodnotě.

Nejprve se podíváme, jak se funkce srovnají v levém krajním bodu I: f (0) = 1 a g(0) = 0. Proto f (0) > g(0), to je dobrý začátek. Teď porovnáme jejich derivace na vnitřku I. Máme f ′(t) = e^t a g′(t) = 2. Kdyby byla vždy (pro kladná t) f ′ alespoň stejně velká jako g′, pak by funkce f začínala větší na levém konci I a rostla minimálně stejně rychle jako g, tudíž by byla větší na celém I. Bohužel to není pravda, pro malá kladná t je e^t menší než 2. Funkce g tedy na začátku intervalu I roste rychleji, takže je klidně možné, že funkci f dožene a předžene, než zase začne růst rychleji f. Tento přístup tedy selhal.

Poznámka: Uvažujme funkci h(t) = t. Zase máme f (0) > h(0), ale teď už také f ′ > h′ pro t > 0, neboť h′(t) = 1. Onen výše použitý algoritmus už tedy teď funguje a dokazuje, že vlastně e^t > t na intervalu I. Všimněte si, že exponenciála je vždy kladná, tudíž ta nerovnost triviálně platí také pro záporná t. Máme tedy e^t > t pro všechna reálná t. Podobně také máme e^t > 2t pro záporná t.

To nás přivádí zpět k našemu problému. Co tedy s tou nepříjemnou dvojkou v g? Všimněte si, že zadaná otázka je vlastně otázkou na to, jak rychle roste přímka 2t, zda dokáže protnout graf exponenciály nebo ne. Viděli jsme, že přímka daná rovnicí t to nestačí, evidentně koeficient (směrnice) 1 není dostatečně velký. Pokud tuto směrnici začneme zvětšovat, tak přímka začne růst rychleji, nakonec se nejprve dotkne exponenciály a pak (při dalším zvětšení směrnice) ji protne.

(Přímka daná t je zaznačena zeleně. Abychom měli hezčí obrázek, nepoužili jsme na svislé a vodorovné ose stejné měřítko.) Jak tam zapadne daná přímka 2t? To se snadněji nahlédne, když změníme úhel pohledu. Před chvílí jsme vlastně dokázali, že je funkce e^t − t kladná na I (dokonce všude), podobně by stačilo dokázat, že rozdíl d(t) = e^t − 2t je všude kladný (nebo nulový), pak to bude platit tím spíše na I. Jak by se to dalo udělat? Docela snadno, najdeme minimum d a pak se podíváme, jestli je záporné nebo ne.

Na to máme standardní algoritmus. Všimněte si, že na obou koncích (v nekonečnu a mínus nekonečnu) roste funkce e^t − 2t do nekonečna, její globální minimum (či možná více minim) se tedy musí nacházet někde uprostřed, v kritickém bodě. Z derivace d′(t) = e^t − 2 dostáváme jeden, t = ln(2), takže hodnota globálního minima je

d(ln(2)) = e^ln(2) − 2ln(2) = 2 − 2ln(2) = 2[1 − ln(2)] > 0.

To dokazuje, že d je vždy kladné, proto také e^t > 2t pro všechna t.

Bonusový problém: Viděli jsme, že ani přímka daná vzorcem 2t nestihne exponenciálu předehnat, mimochodem na tom obrázku výše je modrá. Z obrázku se ale také zdá, že ještě rychlejší přímky to dokážou. Kde je ta hranice? Přesně řečeno, pro kterou hodnotu A se přímka daná y = A⋅t dotkne exponenciály?

Opět použijeme přístup přes minimum. Uděláme si k tomu obrázek. My se vlastně díváme na následující křivky, reprezentující rozdíly mezi exponenciálou a různými přímkami A⋅t, a zajímá nás, která má minimum rovno nule.

Postupujeme jako předtím. Nejprve uvažujeme funkci (s parametrem A) danou vzorcem d(t) = e^t − At. Její derivace je d′(t) = e^t − A, řešením rovnice d′(t) = 0 dostaneme jediný kritický bod t = ln(A). Udává, kde se nabývá globální mnimum funkce d, jehož hodnota pak je d(ln(A)) = e^ln(A) − A⋅ln(A) = A − A⋅ln(A) = A⋅(1 − ln(A)). Vidíme, že toto minimum se rovná nule, přesně když ln(A) = 1, tj. pro A = e.

Závěr: Přímka daná y = e⋅t se dotýká exponenciály. Pro 0 < A < e leží přímky y = A⋅t pod exponenciálou, pro A > e tyto přímky protínají exponenciálu ve dvou bodech.

Další příklad
Zpět na Řešené příklady - Věta o střední hodnotě