Theorem.
If a series
Moreover, then we also have the estimate
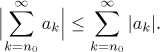
Definition.
Consider a series∑ ak. We say that it converges absolutely, or that it is absolutely convergent, if the series∑ |ak| converges.
What is the relationship between this definition and the usual convergence? First, we see that if we have a series whose terms are all positive (or zero), then the absolute value makes no difference. Therefore for such series the notion of absolute convergence coincides with the notion of convergence. However, for a general series it is different. If a series has some negative terms, the absolute value changes all minuses into pluses and we get a different series. Is its convergence somehow related to the convergence of the original series, or vice versa?
Theorem.
If a series∑ ak converges absolutely, then it necessarily converges.
Moreover, then we also have the estimate
This inequality is actually a generalization of the classical "triangle
inequality"
We see that the notion of absolute convergence is stronger than the usual convergence; it is a "better convergence". The statement can be also turned around. If a sequence is divergent, then it cannot be absolutely convergent. However, implications in opposite directions are not true in general. In other words, if we learn that absolute convergence fails for some series, then it does not help us in determining its convergence. Or, a convergent series may or may not be absolutely convergent (see examples below).
Thus we have the following picture. Imagine the set of all possible series. Some of them are "better", they are convergent. Among these some are even "better" yet, they are absolutely convergent. Those in the middle, convergent but not absolutely convergent, deserve a name.
Definition.
We say that a series is conditionally convergent, or that it converges conditionally, if it converges but not absolutely.
The word "conditionally" suggests that such a series converges, but barely, and it is easy to spoil it. Absolute convergence is much more robust, it can survive quite a lot. For some statements that justify this feeling see the Theorems below.
Examples:
1. The series
![]() is divergent.
is divergent.
And that's it, in particular it cannot be absolutely convergent.
2.
The series
![]() is convergent
(see the Example for Alternating
series test in Theory - Testing convergence - Convergence of general
series), but when we apply absolute value to individual terms, we
get the harmonic series that is
know to diverge.
is convergent
(see the Example for Alternating
series test in Theory - Testing convergence - Convergence of general
series), but when we apply absolute value to individual terms, we
get the harmonic series that is
know to diverge.
Therefore
![]() is not
absolutely convergent, it converges conditionally.
is not
absolutely convergent, it converges conditionally.
3.
The series
![]() is convergent
(this can be easily proved using the
Alternating series test). Is
it also absolutely convergent? If we apply absolute value to all terms, we
get the series
is convergent
(this can be easily proved using the
Alternating series test). Is
it also absolutely convergent? If we apply absolute value to all terms, we
get the series
![]() which we know
is also convergent, see the appropriate example in Theory -
Important examples.
which we know
is also convergent, see the appropriate example in Theory -
Important examples.
Thus the series
![]() converges absolutely.
converges absolutely.
We start with the following handy facts.
Fact.
(i) The scalar multiple of any absolutely convergent series again converges absolutely.
(ii) The sum of two absolutely convergent series also converges absolutely.
(iii) If at least one of two given convergent series also converges absolutely, then their Cauchy product also converges.
(iv) The Cauchy product of two absolutely convergent series also converges absolutely.
We hinted above that absolute convergence is substantially better than mere convergence (that is, conditional convergence). We will show three theorems that justify this opinion.
Theorem.
Assume that∑ ak is a convergent series.
(i) If it converges absolutely, then also the series∑ εkak converges for any choice of signsεk = ±1.
(ii) If it converges conditionally, then there exists a choice of signsεk = ±1 such that∑ εkak = ∞.
The statement (ii) is actually not so surprising. If the given series is not absolutely convergent, then by changing all signs to plus we get a series with infinite sum. The next statement is also not so surprising.
Theorem.
Assume that ∑ ak is a convergent series.
(i) If it converges absolutely, then also every subseries converges.
(ii) If it converges conditionally, then there exists a subseries of this series that diverges to infinity.
For instance, we have already commented that if we take all odd terms in the above alternating harmonic series (Example 2), then we get a divergent series.
I left the real beauty for the last.
Theorem.
Assume that∑ ak is a convergent series.
(i) If it converges absolutely, then also every reordering of this series converges, and its sum is the same as the sum of the original series.
(ii) If it converges conditionally, then for every constant c real or plus/minus infinity there exists a reordering satisfying∑ aP(k) = c.
I have to admit that when I learned about this, I just said: "Wow!"
Notice
that reordering means that you keep all terms, including their signs, you
just rearrange the order in which they are summed up. This says
that we can take for instance this wonderful series
![]() that we now know to be conditionally convergent, and just by changing the
order of its summands make it sum up to infinity. And if we reorder the very
same numbers in a different way, then the new series will sum up to minus
infinity. Or to 13, or to whichever other number you decide to choose. Weird but
true. This conclusively shows that adding up infinitely many numbers is
really different from adding up finitely many numbers, in particular one
cannot expect to have a general commutative law. This amazing statement (ii)
is sometimes called the Riemann theorem.
that we now know to be conditionally convergent, and just by changing the
order of its summands make it sum up to infinity. And if we reorder the very
same numbers in a different way, then the new series will sum up to minus
infinity. Or to 13, or to whichever other number you decide to choose. Weird but
true. This conclusively shows that adding up infinitely many numbers is
really different from adding up finitely many numbers, in particular one
cannot expect to have a general commutative law. This amazing statement (ii)
is sometimes called the Riemann theorem.
On the other hand, we see why absolute convergence is so popular: It gives you a lot of freedom, for instance you need not worry about rearranging terms, the series will always go to the same number.
Remark: There is also the notion of unconditional convergence. We say that a given series converges unconditionally if every its reordering also converges. It can be proved that this requirement is equivalent to another one: A series converges unconditionally if it converges no matter what signs we put in front of individual terms.
The theorems we saw above show that for real series, these two properties are in turn equivalent to the series being absolutely convergent. They are also the same thing for series with complex numbers and in fact for series in any finitely dimensional space, but they differ in infinitely dimensional spaces, which is way above the level of Math Tutor and so we will ignore it. In "our" world these notions are equivalent and absolute convergence is way easier to work with than unconditional convergence, so pretty much nobody uses the latter. We will do one exception and use it now: We can say that every convergent series either converges conditionally or it converges unconditionally. I think it sounds better than the pair "conditional - absolute" that people use.
Remark on commutativity: The last theorem says that when working with a convergent series (when we do not know whether it converges absolutely or conditionally), we cannot afford to rearrange its terms. On the other hand, with absolutely convergent series we can do this and more. How about this: We are given a series and we split it into two subseries that we then add again. Can we expect to get the same total? A theorem above says that not in general, since the subseries that we create may diverge. On the other hand, there is no problem if the original series is absolutely convergent, then we can even rearrange the order. By induction this can be extended to the case of more series, we get the following statement.
We can take the sum of several absolutely convergent series, take all the terms from all the series involved in it, put them on one heap, redistribute them into brand new series and sum them up - without changing the outcome.