Convergence of general series

While there are quite a few tests for series with non-negative terms, most of that is lost once we allow some sign changes in the series. There are very few tests that would work for general series. We start with those, then we look at the Alternating series test, discuss absolute convergence and conclude this section with Abel's test and Dirichlet's test.

The simplest general test is the

Necessary condition for convergence.
If a sequence {a_k} does not tend to zero, then the series  ∑ a_k  diverges.

(See Basic properties in Theory - Introduction.) However, this is only an implication and unfortunately it helps only very rarely. More useful (although definitely not universally applicable) are versions of the popular Root and Ratio tests for general series.

Theorem (Root test for general series).
Consider a series  ∑ a_k.  Assume that the limit

converges.
• If ϱ < 1 then the series converges.
• If ϱ > 1 then the series diverges.

Theorem (Ratio test for general series).
Consider a series  ∑ a_k.  Assume that the limit

converges.
• If λ < 1 then the series converges.
• If λ > 1 then the series diverges.

(See the Note at the end of the section Root and Ratio tests in Theory - Testing convergence.) As usual, when the two constants end up being 1, then we cannot say anything about the given series.

Alternating series test

Often we have a case when the signs in the series change ...+ − + − +... (that is, the series is alternating) and the terms decrease in absolute value. In that case the situation is the best possible, since then we have a simple test of convergence that gives complete information.

Theorem (Alternating series test, AST).
Consider a series that can be expressed as  ∑ (−1)^kb_k  for some positive b_k that form a non-increasing sequence.
This series converges if and only if, the sequence {b_k} tends to 0.

Note that one direction in this theorem is trivial. If the numbers b_k do not go to zero, then also the terms of the series a_k = (−1)^kb_k do not go to zero and therefore the series diverges by the necessary condition for convergence. On the other hand, if we know that the terms a_k do go to zero, then in general we cannot conclude anything, but in the alternating situation as above it is already enough to show convergence. That is the important thing about the above test.

Note that the above test also applies to alternating series whose signs go in the opposite way, formally (−1)^k+1b_k for some positive b_k (that is, we subtract every even term instead of every odd term in the series). Indeed, given such a series, we can factor one minus sign out of the whole series, then we get a new series whose signs go according to the pattern in the above test and whose convergence is equivalent to convergence of the given series.

Example: Investigate convergence of the series

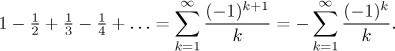
We see that every term of the given series can be expressed as (−1)^k+1b_k for b_k = 1/k > 0. After factoring out one minus we get a series whose terms are now (−1)^kb_k, so there is really no real difference between these two forms. We can apply the Alternating series test: The sequence {1/k} is decreasing and tends to 0, therefore by this test the given series converges.

Note that we could have changed the given series into a "proper alternating series" also by reindexing like this:

Then we would use the AST with b_n = 1/(n − 1).

Some examples can be found in Solved Problems - Testing convergence, namely this problem and this problem.

In more advanced courses students learn some less popular tests that can help also with other combinations of signs than the alternating situation. At the end of this section we cover Dirichlet's test that can be though of as a generalization of AST for more complicated patterns of signs.

Of course, in a situation when terms in a series change signs one would have to be really lucky to get an alternating series, since there are many ways in which the signs may change. Then we cannot use AST, even if the changes follow a regular pattern (for instance two pluses always followed by one minus or something like this). Note that in the "+ + −" situation even the more general Dirichlet test below fails, so sings can easily get really troublesome. What can we do when the general tests from the first part of this section also fail? One fairly obvious idea is to get rid of the signs by applying absolute value to all terms of the series. Then we can use all those wonderful tests, but unfortunately we apply it to a different series than the one that we investigate. Fortunately for us, there is a one-way connection.

If we find that the series  ∑ |a_k|  converges, then also the given series  ∑ a_k  converges (this was a theorem in Theory - Introduction - Absolute convergence). This means that we have to rely on luck. We are given a series whose signs change (and not in the alternating way above), we apply tests to its version with absolute values and if we are lucky, we get convergence, then also our original series converges.

However, it may also happen that the series with absolute values diverges and then we do not know anything about convergence of the given series. There are no general guidelines concerning such a situation, every series is an individual problem and all depends on our experience, we try to find some trick to decide its convergence.

Sometimes one can use one of the following two tests.

The following test allows us to take a series that we know to converge and modify it without losing its convergence.

Theorem (Abel's test).
Consider a convergent series  ∑ a_k. Assume that {b_k} is a monotone and convergent sequence. Then also the series  ∑ a_kb_k  converges.

In fact, Abel's test can be deduced from the following, more general criterion.

Theorem (Dirichlet's test).
Consider a series  ∑ a_k  such that all its partial sums are bounded; that is, there exists some M so that for all N one has

Assume that {b_k} is a non-increasing sequence of positive numbers that tends to 0. Then the series  ∑ a_kb_k  converges.

For examples see this problem and this problem in Solved problems - Testing convergence.

This test can be used in a wide range of situations, but one particular situation is worth exploring closer. Note that this test also implies the Alternating series test above. Indeed, consider the situation as in the assumptions of AST. We have some positive numbers b_k that are non-increasing and go to zero. Now we form an alternating series from them, which we can interpret as follows: We create a series with terms a_kb_k, where a_k = (−1)^k. We know that partial sums of 1 + 1 − 1 + ... are either 1 or 0, so they are bounded and the numbers a_k satisfy assumptions of the Dirichlet test, the same is true for numbers b_k and we get convergence.

We have just explained why Dirichlet's test generalizes the AST, but it is interesting to return to this situation and explore it a bit more. We claim that when we start with positive numbers b_k that are non-increasing and go to zero, then the Dirichlet test allows us to modify them by signs also in other ways than just alternating. Indeed, assume that terms a_k are numbers −1 and 1 that are chosen in such a way that a certain pattern is repeated over and over (a periodic sequence so to speak). If in that basic pattern there is equal number of minuses and pluses, then partial sums can again attain only finitely many distinct values, so they are bounded and the Dirichlet test gives convergence. This is definitely a significant improvement over the rather special Alternating series test. We conclude this section by stating this generalization of AST properly.

Fact.
Consider numbers a_k = ±1. Assume that there is T > 0 such that a_kT+i = a_i for all natural numbers k and integers i satisfying 0 ≤ i < T. Let

a₁ + a₂ + ... + a_T = 0.

Assume that {b_k} is a non-increasing sequence of positive numbers that tends to 0. Then the series  ∑ a_kb_k  converges.

Back to Theory - Testing convergence