Úvod

Zde uvedeme pojem posloupnosti. Začneme intuitivním přístupem a explicitní definicí, pak ukážeme rekurzivní definici a definujeme podposloupnost.

Co je to posloupnost? Je možno odpovědět dvojím způsobem, přesně a pochopitelně. Začneme s přesnou definicí, ale pokud vás nezajímá, přeskočte k příkladu za ní.

Definice.
Posloupností rozumíme libovolné zobrazení z množiny přirozených čísel do množiny reálných čísel.

Vlastně bychom měli psát "reálné posloupnosti" či "posloupnosti reálných čísel", protože jsou i jiné. Ty se ale v základním kursu kalkulu neprobírají, takže se obvykle říká prostě jen "posloupnosti".

Protože takováto zobrazení pouze přijímají přirozená čísla jako argument, je zvykem značit posloupnosti trochu jinak než obvykle zobrazení píšeme. Je možné vypsat hodnoty T pro n rovno 1,2,3,..., to jest můžeme psát {T(1), T(2), T(3),...}. Abychom dále zdůraznili, že jde o posloupnost, namísto T(n) píšeme a_n, takže lze celou posloupnost "vypsat" takto ve správném pořadí: {a₁, a₂, a₃, a₄, ...}, krátce píšeme nebo {a_n}_n=1,2,3,.... Poznamenejme, že někdy za n v indexu dosazujeme vzorce a pak by mohlo být nešikovné to psát jako dolní index; v takových případech píšeme a(n) namísto a_n.

Příklad: Vzorce ,   {2n − 1}_n=1,2,3,...   nebo a_n = 2n − 1, n = 1,2,3,... všechny definují tutéž posloupnost, jmenovitě posloupnost {1, 3, 5, 7, 9, 11,...}. Ze vzorce skutečně hravě spočítáme, že a₁ = 1, a₂ = 3, a₃ = 5, a₄ = 7 atd, takže když seřadíme všechna a_n s n procházejícím přirozenými čísly za sebe, začne to 1, 3, 5, 7,...

Všechny tři definice v našem příkladě mají jedno společné: poskytují vzorec, který nám umožňuje spočítat přímo libovolný člen dané posloupnosti. Například její desátý člen je a₁₀ = 2⋅10 − 1 = 19.

Ono další vyjádření posloupnosti, výpis (či seznam), je zrádné, protože nespecifikuje, jak vypadají další členy. Samozřejmě že odhadneme, že další člen po 11 má být 13, ale nemůžeme si být jisti. Toto značení se proto používá jen jako pomocné, když chceme získat představu, jak dotyčná posloupnost vypadá. Hodně z vlastností posloupnosti je také možné odhadnout tím, že si nakreslíme její graf. V našem případě vypadá takto:

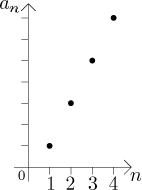
Stejně jako výpis, ani graf není spolehlivý, protože si nikdy nemůžeme být jistí, co posloupnost udělá, poté co uteče z obrázku. Výpis i graf by totiž měly pokračovat do nekonečna, aby ukázaly všechny členy posloupnosti, ale to je evidentně nemožné. Obvykle vypíšeme či nakreslíme dostatečný počet členů posloupnosti, aby se vyznačily její obecné tendence (pokud nějaké jsou), rozumí se, že posloupnost dále pokračuje (jak se n probírá do nekonečna přirozenými čísly) naznačeným způsobem.

Je ještě jiný způsob, jak si zviditelnit posloupnosti. Teď to asi nebude nějak výhodnější, ale bude se to hodit později, až začneme zkoumat funkce. Tento způsob je popsán v této poznámce.

Mimochodem, kdybychom chtěli definovat posloupnost z našeho příkladu podle definice, použili bychom zobrazení T(n) = 2n − 1. Jak už bylo vidět, ve skutečnosti ale při práci s posloupnosti toto T nepotřebujeme (a je méně pohodlná), takže formální definici ignorujeme.

Teď už jsme připraveni na intuitivní definici posloupnosti:

Posloupností rozumíme nekonečnou, ale spočetnou množinu reálných čísel, u kterých je rovněž určeno pořadí, v jakém jdou za sebou.

V našem příkladě je daná posloupnost prostě jen množina všech lichých přirozených čísel, která jsou seřazena podle velikosti od nejmenšího. To podstatné na posloupnosti jsou právě ony hodnoty a jejich pořadí. Ačkoliv už jsme se zmínili, že výpis (a graf) nejsou spolehlivé při zkoumání posloupností, je fakt, že výpis vlastně přesně vystihuje, co je to posloupnost. Vzorce jsou nutné pro přesné výpočty, ale ty jsou jen pokusem zapsat matematicky podstatu dané posloupnosti a ani nejsou jednoznačné.

Náš příklad a vzorec {a_n} byl asi tím nejpřirozenějším způsobem, jak zapsat všechna lichá přirozená čísla. Uvedli jsme, že pořadí je důležité, a je přirozené to vyjádřit takto: 1 je první, 3 je druhá, 5 je třetí atd. Proto je očíslování a₁ = 1, a₂ = 3, a₃ = 5,... použité výše zcela přirozené, pak už jen zbývá najít nějaký vzorec, který vyrobí třeba 7 z indexu n = 4. Je nicméně také pravda, že takovéto očíslování není jediné možné. Je například možné číslovat členy této posloupnosti jako "nultý, první, druhý, třetí,...", neboli matematicky zapsáno, b₀ = 1, b₁ = 3, b₂ = 5,...

Posloupnost daná vzorcem b_m = 2m + 1, m = 0,1,2,... vypadá na první pohled jako něco jiného než naše posloupnost a_n, ve skutečnosti ale dává toto nové značení stejnou posloupnost: {1, 3, 5, 7, 9,...} (ověřte). Jediný rozdíl je v tom, že podle nového vzorce má řekněme člen 9 index m = 4, zatímco předtím měl index n = 5. Tímto znovu zdůrazňujeme, že to důležité jsou čísla (členy posloupnosti) a jejich pořadí; jak je očíslujeme a jak je vyjádříme vzorcem je druhořadé. To důležité tedy je, že číslo 9 je členem dané posloupnosti, že jde po čísle 7 a před 11.

Je samozřejmě možné modifikovat formální definici posloupnosti, aby také umožnila tyto jiné formy indexování, ale zkomplikovala by se tím, takže většině učebnic to nestojí za to. V praxi ji stejně nepoužíváme.

Poučením je, že tatáž posloupnost může mít mnoho rozdílných popisů, občas je dokonce dost těžké už jen rozpoznat, že dva popisy dávají tutéž posloupnost. Člověk by se tedy neměl příliš upínat na jeden konkrétní vzorec, spíše se snažit soustředit na to, co znamená. Výpis (a graf) často dají jakési ponětí o základních vlastnostech dané posloupnosti, což je pak v případě potřeby možné potvrdit matematicky pomocí nějakého popisu vzorcem. To platí zejména o očíslování. Zatímco indexování 1,2,3,... je přirozené, lidé často dávají přednost jinému, asi druhé nejpopulárnější je ono 0,1,2,... (viz například geometrická posloupnost a geometrická řada).

Často je nám dokonce jedno, kterým číslem začínáme indexovat. V takovém případě prostě zcela vynecháme odkaz na číslování, protože se předpokládá, že vždycky k indexaci používáme celých čísel, počínaje nějakým určitý číslem. Pak často píšeme jen {a_n}.

Teď si ukážeme příklad, kdy máme velmi dobrý důvod, proč indexovat 2,3,4,... Uvažujme posloupnost c_n = 1/ln(n), n = 2,3,4,..., kterou můžeme také zapsat takto: .

Je zřejmé, že číslo n = 1 nejde do vzorce dosadit. Posloupnost vypadá takto:

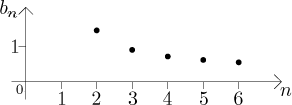
Poznamenejme, že kdybychom opravdu chtěli, tak dokážeme tuto posloupnost indexovat m = 1,2,3,..., pak bychom ale museli použít vzorec 1/ln(m+1). Dostali bychom tatáž čísla ve stejném pořadí: {1/ln(2), 1/ln(3), 1/ln(4),...}. Všimněte si, že v tomto novém značení se poněkud změní graf, jmenovitě se posune o jedno doleva. Toto naznačuje, že grafy tohoto typu jsou závislé na indexování, a proto přesná pozice bodů v grafu není až tak důležitá. Pokud se daný graf posune doleva či doprava o určitou celočíselnou hodnotu, posloupnost, kterou znázorňuje, bude pořád stejná, jen s jiným indexováním. Na bodech jsou tedy důležité jen jejich hodnoty y a jejich pořadí.

V předcházejících příkladech jsme viděli nejběžnější metodu zadávání poslouností: nějakým matematickým vzorcem, ve kterém se vyskytuje n. Tomuto způsobu se říká explicitní definice. Jsou i jiné způsoby. Nejprve ukážeme "definici" výpisem.

Příklad: {3, π, 2, 2, −1, 0, −1, 0, 2.5,...}, n = 0,1,2,...
Začali jsme číslování nulou, takže pokud označíme členy posloupnosti jako d, máme d₀ = 3, d₁ = π, a tak dále. Nezdá se, že by šlo tuto posloupnost vyjádřit nějakým vzorcem, nicméně pořád je to posloupnost. Zde je její graf:

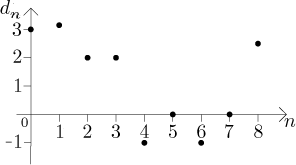
Alternativní graf této posloupnosti je k vidění v této poznámce.

S takovouto definicí se často nestřetáváme; důvodem, je, že to vlastně definice není. Nepodařilo se nám totiž definovat celou posloupnost. Víme například, že d₈ = 2.5, ale nevíme, kolik je d₉. Abychom z toho udělali správnou definici, museli bychom nějak specifikovat i ostatní členy (a těch je nekonečně mnoho, takže to nepůjde výpisem).

Jak jsme již předeslali, výpis se používá jen jako nástroj k intuitivnímu náhledu na obsah posloupnosti. Při neformálním výkladu se občas použije jako odkaz na jednoduché známé posloupnosti, asi nejčastější je "1,2,3,..." jako specifikace přirozených čísel, ale měli bychom tím spíš šetřit. Rozhodně bychom se tomu měli vyhýbat při formálním zápisu. Konec konců, když napíšeme "posloupnost lichých přirozených čísel", tak je hned jasné, oč jde. Naopak když čtenář vidí {1, 3, 5, 7,...} bez dalšího komentáře, tak ho samozřejmě napadne, že další člen je 9, ale nemůže si být jistý, jestli to třeba nemá být 11, protože jde o výpis lichých přirozených čísel, která nejsou složená.

V následující sekci se podíváme na další způsob zadání poslouposti, tentokráte již správný.

Rekurzivní definice funguje následovně: Specifikujeme vzorec, pomocí kterého lze obdržet určitý člen definované posloupnosti za předpokladu, že známe členy předchozí. Samozřejmě také musíme specifikovat dostatečný počet prvních členů, aby šlo proceduru začít.

Příklad: Posloupnost z našeho prvního příkladu, {2n − 1}_n=1,2,3,... = {1, 3, 5, 7,...} může být také zadána následujícími dvěma podmínkami:
(1)    e₁ = 1,
(2)    e_n+1 = e_n + 2, n = 1,2,3,...

A opravdu, první člen se shoduje, e₁ = a₁. Pomocí rekurzivní rovnice (2) s n = 1 dostaneme

e₂ = e₁ + 2 = 1 + 2 = 3 = a₂.

Rekurzivní rovnice s n = 2 pak dává

e₃ = e₂ + 2 = 3 + 2 = 5 = a₃.

Když se dál pokračuje tímto způsobem, lze se přesvědčit, že první členy těchto dvou posloupností jsou shodné, takže lze také doufat, že posloupnosti jsou stejné. To jde i dokázat matematickou indukcí.

Je možné zkusit i jinou rekurzivní definici téže posloupnosti:
(1)    g₁ = 1, g₂ = 3, g₃ = 5,
(2)    g_n+1 = 2g_n − g_n−2 − 2, n = 3,4,5,...

První tři členy se zase shodují: g₁ = a₁, g₂ = a₂, g₃ = a₃. Ke kontrole dalšího členu použijeme rekurzivní vzorec s n = 3:

g₄ = 2g₃ − g₁ − 2 = 2⋅5 − 1 − 2 = 7 = a₄.

A tak dále.

Hned takto vidíme hlavní rozdíl mezi explicitní a rekurzivní definicí: Rekurzivní definice nám nedovoluje spočítat přímo určitý člen posloupnosti. Přesto je každý člen jednoznačně určen (na rozdíl od "definice" výpisem), takže rekurze je korektním způsobem definice. Mnoho posloupností je možné zadat jak explicitně, tak rekurzivně, ale neexistuje standardní či zjevný způsob, jak přejít z jednoho způsobu na druhý, není dokonce ani standardní způsob kontroly, že dva popisy definují tutéž posloupnost.

Ačkoliv obvykle dáváme přednost explicitní definici (je praktičtější), některé posloupnosti je lepší vyjádřit rekurzivně a některé posloupnosti ani jinak vyjádřit neumíme; někdy tato definice také umožní lépe pochopit, oč v dané posloupnosti jde. Podívejme se na následující posloupnost.

Příklad: Fibonacciho posloupnost je dána vztahy
(1)    f₁ = 1, f₂ = 1,
(2)    f_n+1 = f_n + f_n−1, n = 2,3,4,...

Řečeno slovy, každý člen (kromě prvních dvou) je součtem dvou předchozích členů. Posloupnost jde {1, 1, 2, 3, 5, 8, 13,...}. Existuje i explicitní vyjádření, ale příslušný vzorec je dost hnusný. Tuto posloupnost zavedl Fibonacci (z Pisy v Itálii) v roce 1202 (ve spise o aritmetrice Liber abaci) k popisu růstu populace.

Posloupnost je uspořádaná množina čísel. Když je nějaká dána, její podposloupnost obdržíme tak, že vybereme nějaké členy z dané posloupnosti a seřadíme je podle původního pořadí. Například z posloupnosti {1, 3, 5, 7,...} lichých čísel můžeme vybrat třeba podposloupnost {1, 5, 7, 13, 137, 345,...}. Nebo podposloupnost {1, 3, 7, 9, 13, 15, 19, 21,...}. Nebo mnoho jiných.
A teď formální definice:

Definice.
Nechť {a_n} je posloupnost. Její podposloupnost obdržíme tím, že vybereme nějaká čísla k₁ < k₂ < k₃ <... z indexovací množiny dané posloupnosti a uvažujeme posloupnost .

Příklad: Uvažujme posloupnost a_n = n − 1, n = 1,2,3,..., tedy {0, 1, 2, 3, 4,...}.
Teď vybereme podposloupnost. Vybereme čísla 1 < 3 < 5 < 7 <... (toto jsou indexy členů původní posloupnosti, které budou vybrány, aby vytvořily naší podposloupnost), a tak obdržíme podposloupnost {a₁, a₃, a₅,...}; to jest {0, 2, 4,...}.

Základní vlastnosti
Zpět na Teorie - Úvod