Důležité příklady
V této části probereme základní příklady posloupností a podíváme se na jejich
omezenost a monotonii. Začneme alternující posloupností, ke které se ještě
vrátíme
na konci, stručně probereme
aritmetické posloupnosti, nejdůležitějším
typem ale je
geometrická posloupnost. K těmto
příkladům se ještě vrátíme v části Teorie - Limita -
Důležité příklady.
Alternující posloupnost
Alternující posloupnost je vlastně kategorie, obecnější typ posloupnosti (viz
konec této části), ale zde se podíváme na
posloupnost, která je jakýmsi prototypem alternující posloupnosti:
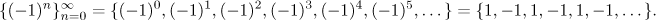
Graf vypadá takto:
Z obrázku hned vidíme, že tato posloupnost je omezená (pro všechna n
evidentně máme |(−1)n| ≤ 1) a není monotonní.
Nemůže být rostoucí či neklesající, protože druhý člen (když
n = 1) je menší než první člen (když
n = 0), takže tam posloupnost klesne; nemůže také být
klesající nebo nerostoucí, protože třetí člen je větší než druhý člen,
neboli tam posloupnost vzroste.
Je také možné indexovat tuto posloupnost od
n = 1. Jsou dva
důvody pro začátek od nuly, jak jsme to zde udělali. První důvod je má
preference - prostě se mi líbí víc, když posloupnost začne kladným číslem
než číslem −1, a občas je to dokonce takto pohodlnější. Druhý důvod bude
jasnější, když dojde řeč na geometrickou řadu.
Tato posloupnost se objevuje docela často; někdy sama o sobě, ale častěji
jako součást jiné posloupnosti; viz poslední sekce níže.
Aritmetická posloupnost
Definice.
Aritmetickou posloupností rozumíme libovolnou posloupnost typu
an = a + nd,
n = 0,1,2,3,...
kde a a d jsou libovolná pevně zvolená reálná čísla.
Aritmetická posloupnost tedy vypadá takto:
{a, a + d, a + 2d,
a + 3d, a + 4d,...}.
Je zase možné indexovat tuto posloupnost
n = 1,2,3,..., ale
pak by bylo prvním členem posloupnosti číslo a+d, což není tak
pěkné jako začínat s a.
Všimněte si následujícího: každý člen aritmetické posloupnosti lze získat
přičtením konstanty d k předchozímu členu. Například
a5 = a + 5d = (a + 4d) + d = a4 + d.
To je základní myšlenka aritmetické posloupnosti. Začne se nějakým číslem
a a pak se přičítá zas a zas stejný rozdíl d. Nemělo by tedy
překvapit, že aritmetická posloupnost může být tedy definována
rekurzivně
takto:
(1) a0 = a,
(2)
an+1 = an + d,
n = 0,1,2,3,...
Není těžké dokázat indukcí, že jak explicitní, tak rekurzivní definice
definují tutéž posloupnost.
Poslední charakterizace aritmetické posloupnosti: Daná posloupnost je
aritmetická právě tehdy, je-li rozdíl mezi dvěma následujícími členy stále
stejný.
Příklad:
{2, 0.5, −1, −2.5, −4, −5.5,...} je aritmetická posloupnost. Opravdu,
rozdíl mezi následujícími členy je vždy
d = −1.5. Ověřte, že pro
n = 0,1,2,3,.. jsou členy posloupnosti dány vzorcem
an = 2 + (−1.5)n.
Zvolili jsme tento příklad, abychom ukázali, že krok d může také být
záporný. Je jeden speciální případ, a to když
d = 0. Pak
an = a pro všechna n a dostaneme
konstantní posloupnost {a, a, a,...}.
Jaké jsou vlastnosti aritmetické posloupnosti? Nejprve se podíváme na
triviální případ konstantní posloupnosti
an = a
pro všechna n.
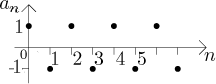
Hned vidíme, že taková posloupnost je omezená; navíc je monotonní, jmenovitě
zároveň neklesající a nerostoucí.
Co se stane pro d nenulové? Jsou dva případy.
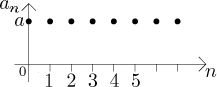
Případ 1: Jestliže d > 0, pak je posloupnost
rostoucí (a také neklesající), neboť
an+1 = an + d > an.
Z odhadu
an = a + nd > a
také vidíme, že takováto posloupnost je omezená zdola. Na druhou stranu
není omezená shora a tudíž není
omezená.
Případ 2: Jestliže d < 0, pak je posloupnost
klesající (a také nerostoucí), neboť
an+1 = an + d < an.
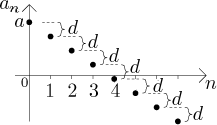
Z odhadu
an = a + nd < a
také vidíme, že takováto posloupnost je omezená shora. Na druhou stranu není
omezená zdola (důkaz je podobný předchozímu případu), tudíž není ani omezená.
Geometrická posloupnost
Definice.
Geometrickou posloupností rozumíme libovolnou posloupnost typu
an = aqn,
n = 0,1,2,3,...
kde a z q jsou pevně zvolená reálná čísla.
Geometrická posloupnost tedy vypadá takto (máme
aq0 = a⋅1 = a):
{a, aq, aq2,
aq3, aq4,...}.
Je zase možné indexovat tuto posloupnost
n = 1,2,3,..., pak
by ale bylo jejím prvním členem číslo aq, což není tak pěkné jako
začínat členem a. Ve většině případů máme dokonce
a = 1, takže typická geometrická posloupnost vypadá takto:
{1, q, q2,
q3, q4,...}.
Jeden příklad geometrické posloupnosti jsme už viděli, jmenovitě onen
prototyp alternující posloupnosti na začátku.
Všimněte si, že každý člen geometrické posloupnosti lze získat vynásobením
předchozího členu konstantou q. Například
a5 = aq5 = (aq4)q = a4q.
To je základní myšlenka geometrické posloupnosti. Začnete nějakým číslem a
pak jej zas a zas násobíte touže konstantou q. Nemělo by tedy
překvapit, že geometrickou posloupnost lze také definovat
rekurzivně takto:
(1) a0 = a,
(2)
an+1 = anq,
n = 0,1,2,3,...
Není těžké dokázat indukcí, že jak explicitní, tak rekurzivní definice
definují tutéž nekonečnou posloupnost.
Poslední charakterizace geometrické posloupnosti: Daná posloupnost je
geometrická, pokud podíl dvou následujících členů je vždy stejný.
Ten příklad geometrické posloupnosti, který jsme viděli dříve (alternující
posloupnost), je poněkud speciální, a tak není dobrým reprezentantem chování
geometrické posloupnosti. Další výjimkou je případ, kdy
a = q = 1.
Dostaneme posloupnost {1, 1, 1, 1, 1,...}, což je konstantní
posloupnost, na kterou se můžeme dívat také jako na aritmetickou posloupnost.
Je mimochodem docela jednoduché dokázat algebraicky, že pokud je nějaká
geometrická posloupnost konstantní, pak nutně
q = 1 a tato
posloupnost je také aritmetická. Na druhou stranu, jediné posloupnosti,
které jsou zároveň aritmetické a geometrické, jsou konstantní posloupnosti.
Na ně se samozřejmě vztahují příslušné závěry, jsou omezené a monotonní.
Abychom to shrnuli, případy q = −1 a
q = 1
jsou speciální a kdykoliv dojde na geometrickou posloupnost (či geometrickou
řadu), budou se chovat jinak než ty ostatní.
Abychom viděli, co se děje, když je q jiné, se podíváme na čtyři
typické příklady, pro jednoduchost položíme (jako obvykle)
a = 1.
Příklad:
Volba q = 2 dává posloupnost
an = 2n, neboli
{20, 21, 22, 23,
24,...} = {1, 2, 4, 8, 16, 32, 64,...}.
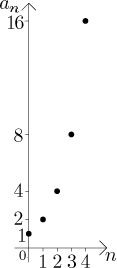
Tato posloupnost je rostoucí, omezená zdola (evidentně
an > 0 pro všechna n) ale není omezená
shora, tedy ani omezená.
Příklad:
Volba q = 1/2 dává posloupnost
an = (1/2)n = 1/2n,
neboli
{1/20, 1/21, 1/22, 1/23,
1/24,...} = {1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64,...}.

Tato posloupnost je klesající, omezená zdola (evidentně
an > 0 pro všechna n) ale také shora
(an ≤ 1 pro všechna
n = 0,1,2,3,...), tedy je omezená.
Tyto dva příklady ukazují dva základní typy geometrické posloupnosti,
jmenovitě když q > 1 a když
0 < q < 1. V následujících dvou příkladech
použijeme tatáž čísla, ale se záporným znaménkem, čímž získáme dva typické
příklady pro záporná q: jmenovitě když
q < −1 a
−1 < q < 0. Protože pro záporná q
můžeme psát q = (−1)|q|, uvidíte, že tyto dva
případy budou vlastně založeny na předchozích dvou, které jsou jen
modifikovány "přilepením znamének" alternující posloupnosti z prvního
příkladu na začátku.
Příklad:
Volba q = −2 dává posloupnost
an = (−2)n = (−1)n2n,
neboli
{20, −21, 22, −23,
24,...} = {1, −2, 4, −8, 16, −32, 64,...}.
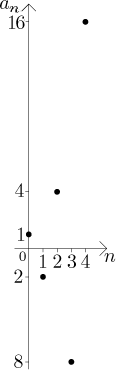
Tato posloupnost není monotonní, není omezená zdola ani shora, tedy ani
omezená.
Příklad:
Volba q = −1/2 dává posloupnost
an = (−1/2)n = (−1)n/2n,
neboli
{1/20, −1/21, 1/22, −1/23,
1/24,...} = {1, −1/2, 1/4, −1/8, 1/16, −1/32, 1/64,...}.
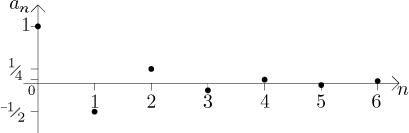
Tato posloupnost není monotonní, je omezená zdola (evidentně
an > −1 pro všechna n) a také shora
(an ≤ 1 pro všechna
n = 0,1,2,3,...), tudíž omezená.
Pro další informaci viz
Důležité příklady v části
Posloupnosti - Teorie - Limita.
Všimněte si, že v těchto posledních dvou příkladech jsme vlastně vzali grafy
předchozích dvou příkladů a přehodili každý druhý člen dolů okolo osy
n. To naznačuje, že při zkoumání posloupností, jejichž znaménka se
mění pravidelně, může být výhodné je nejprve ignorovat. To nás přivádí k
poslednímu tématu.
Alternující posloupnost podruhé
Náš první příklad byl prototypem alternující posloupnosti. Teď se podíváme na
obecnější definici.
Definice.
Alternující posloupností rozumíme libovolnou posloupnost
{an},
kterou je možné zapsat jako
an = (−1)nbn
pro nějaká nezáporná reálná čísla bn.
Mimochodem, spousta lidí by dala přednost začít
indexování nějakým sudým číslem, aby daná alternující posloupnost začínala
plusem; myslím, že řekněme {b0, -b1,
b2, -b3,...} vypadá mnohem lépe.
Ještě stažší je ovšem prostě prohlásit, že coby alternující posloupnosti
uvažujeme i posloupnosti, jejichž členy lze zapsat jako
an = (−1)n+1bn
pro nějaká nezáporná reálná čísla bn.
Pro zjednodušení budeme formalně pracovat s typem z definice, ale vše
samozřejmě funguje i pro tento druhý typ, který má znaménka přesně naopak.
Při vyšetřování alternující posloupnosti
{a1, a2,
a3,...} = {-b1, b2,
-b3,...}
je často jednodušší nejprve ignorovat znaménka a vyšetřovat posloupnost
{b1, b2, b3,...}, pak
teprve vzít ta znaménka v úvahu - už proto, že mnohé metody se dají aplikovat
pouze na posloupnosti s nezápornými členy, takže je možné je použít na onu
posloupnost bez znamének, ale ne pro tu původní alternující. Ignorování
znamének také může pomoci, pokud se snažíme využít vztahu mezi posloupnostmi
a funkcemi (viz
Posloupnosti a funkce v
sekci Teorie - Limita).
Obzvláště při kreslení grafu alternující posloupnosti je obvykle jednodušší
nejdříve vyšetřit tvar grafu {bn}, pak přikreslit
jeho zrcadlový obraz a nakonec nakreslit body alternující posloupnosti tak,
že si střídavě vybíráme z horního a dolního tvaru:
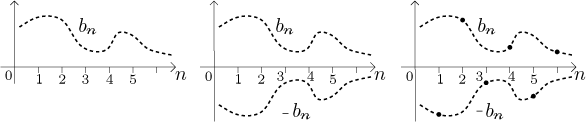
Všimněte si, že tuto ideu je také možné použít na kreslení grafu
posloupností, jejichž znaménka se mění pravidelným způsobem, i když to není
ten alternující. Například
{1, 2, −4, 8, 16, −32, 64,...} je posloupnost
(založena na našem geometrickém příkladě), která není alternující, přesto se
znaménka mění pravidelně; v takových případech je často možné ignorovat
mínusy, kde to přijde vhod, a pak je zase doplnit později.
Poslední poznámka: Existují i posloupnosti, jejichž znaménka nejen
nealternují, ale dokonce ani nemají nějakou pravidelnost; jinými slovy,
neexistuje určitý vzorec znamének, který by se dokola opakoval, a co je
důležitější, ze znalosti určitého počtu členů nemůžeme odvodit, jaké znaménko
má následující člen (tj. jen ze známých znamének, bez přímého výpočtu onoho
členu ze vzorce). Asi nejjednodušší příklad je
{sin(n)}, n = 0,1,2,3,...
(jako obvykle, funkce sinus se bere v radiánech, ne ve
stupních). Posloupnost jde
{sin(1), sin(2), sin(3), sin(4),...}. První tři
členy jsou kladné, ale protože 4 je větší než
π a menší než
2π, je
sin(4) záporný, stejně
jako sin(5) a sin(6), sin(7) je
kladný a tak dále. Dokázat, že žádná
pravidelnost neexistuje, je dosti těžké, musíte mi věřit, ale jakýsi pocit
můžete získat, když si spočítáte prvních řekněme 30 členů. Uvidíte, že
znaménka přichází ve skupinách po třech či čtyřech, ale výskyt skupin po
čtyřech není vůbec pravidelný.
Operace s posloupnostmi
Zpět na Teorie - Úvod
![]()








