Příklad: Prozkoumejte omezenost a monotonii posloupnosti
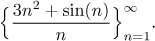
Řešení:
Zkusíme spočítat několik prvních členů:
a1 = 3 + sin(1),
a2 = 6 + sin(2)/2,
a3 = 9 + sin(3)/3,
a4 = 12 + sin(4)/4. Jak velká jsou tato čísla?
Protože
|sin(n)| ≤ 1,
druhý člen v součtu je v absolutní hodnotě vždy nanejvýš
jedna. První sčítanec vypadá, že se vždy zvýší o 3, takže následující člen
posloupnosti je vždy větší než předchozí o hodnotu mezi 1 a 5. Proč? Máme
a1 = 3 ± 1,
a2 = 6 ± 1,
a3 = 9 ± 1,
a4 = 12 ± 1, a tak dále. (Dokonce
máme například a4 = 12 ± 1/4, ale snažší - i
když méně přesný - odhad stačí.) Co to naznačuje? Za prvé, posloupnost asi
jde do nekonečna, tudíž není omezená. Je nicméně asi omezená zdola. Za
druhé, jak jsme viděli, sinová část je malá ve srovnání s růstem o tři na
každém kroku, takže tato posloupnost je zřejmě rostoucí.
Důkaz omezenosti zdola:
Vždy máme
3n2 + sin(n) ≥ 3n2 − 1 ≥ 0
pro přirozená čísla
n, což dokazuje, že posloupnost splňuje
an ≥ 0; jinými slovy, je omezená zdola.
Teď ukážeme, že posloupnost jde do nekonečna, tudíž nemůže být omezená shora,
tedy ani omezená. Dokážeme to pomocí srovnání, viz např.
Přehled Metod - Limita -
Srovnání a oscilace.
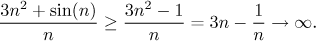
Důkaz monotonie: Ověříme nerovnost pro rostoucí posloupnost.
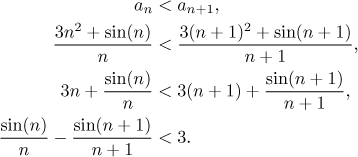
Platí tato nerovnost? To v tomto případě není hned jasné, ale zkusme se
podívat blíže: Sinus je vždy nejvýše 1, takže můžeme odhadovat
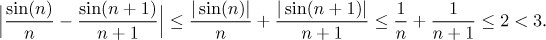
Poslední nerovnost tedy byla pravdivá, proto také platila ta první. Dokázali
jsme, že daná posloupnost je rostoucí.
Mohli bychom použít metody z kalkulu funkcí? Zkusíme to. Podíváme se na
funkci
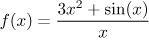 (viz Teorie - Limita -
Posloupnosti a funkce). Najdeme derivaci:
(viz Teorie - Limita -
Posloupnosti a funkce). Najdeme derivaci:
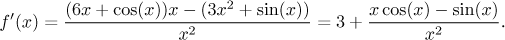
Jako předtím, z omezenosti sinu a kosinu jedničkou odvodíme, že derivace je
nejméně 1 pro x ≥ 1.
Hlavně to znamená,
že je derivace kladná, což znamená, že f
je rostoucí na
(0,∞).
Následně je rostoucí i daná posloupnost.
Poznámka: Zkušený řešič by pracoval raději s výrazem
an = 3n + sin(n)/n,
výpočty jsou pak trochu snažší (derivace docela dost).
Zpět na Řešené příklady - Základní
vlastnosti
![]()
![]()
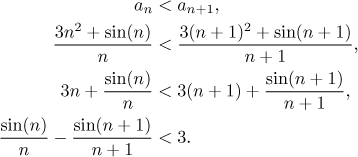
![]()
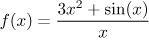 (viz Teorie - Limita -
Posloupnosti a funkce). Najdeme derivaci:
(viz Teorie - Limita -
Posloupnosti a funkce). Najdeme derivaci:
![]()