Šuplík "srovnání a oscilace"

Existuje několik způsobů, jak použít srovnání k nalezení limity. Jsou možná dvě jednostranná srovnání:

1. Uvažujme dvě posloupnosti {a_n} a {b_n}. Jestliže a_n ≤ b_n pro všechna n a a_n→∞, pak také b_n→∞.

2. Uvažujme dvě posloupnosti {a_n} a {b_n}. Jestliže 0 ≤ a_n ≤ b_n pro všechna n a b_n→0, pak také a_n→0.

K získání nenulové limity pomocí srovnání je potřeba dvou omezení:

Věta o sevření:
Uvažujme tři posloupnosti {a_n}, {b_n} a {c_n}, splňující

a_n ≤ b_n ≤ c_n

pro všechna n. Jestliže {a_n} konverguje k nějakému L a {c_n} konverguje k témuž L, pak nutně také {b_n} konverguje k tomuto L.

Věta o sevření - verze s absolutní hodnotou:
Uvažujme dvě posloupnosti {a_n} a {b_n} splňující

|b_n| ≤ a_n

pro všechna n. Jestliže a_n→0, pak také b_n→0.

Použili jsme zde ty nejpopulárnější verze, pro další detaily se podívejte na Teorie - Limita - Limita a srovnání.

Neš začneme s obecným přehledem srovnávací metody, ukážeme si pár příkladů. Výše citovaná tvrzení ohledně srovnání se používají nejčastěji pro jeden z následujících tří důvodů:

Důvod 1. Posloupnost, kterou zkoumáme, obsahuje výraz, který nemá limitu, ale je omezený - neboli výraz, který osciluje. Nejtypičtější příklady jsou

Omezenost naznačí sevření: horní a dolní odhad pro danou posloupnost.

Příklad: Ukážeme, že

Vidíme, že výraz v čitateli má oscilující část, ale máme pro ni omezení. Použijeme tento odhad, abychom našli horní a dolní odhad pro celou posloupnost:

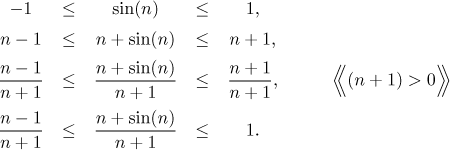
Udělali jsme poznámku o tom, že n + 1 je kladné, protože to znamená, že nemusíme měnit směr nerovností, když tímto číslem dělíme.

Posloupnost nalevo konverguje k 1. To se snadno nahlédne vykrácením n; koneckonců, tento příklad je školní příklad podílu polynomů, viz šuplík polynomy a podíly s mocninami.

Posloupnost napravo také konverguje k 1 (to je triviální). Podle Věty o sevření také daná posloupnost konverguje k 1.

Důvod 2. Většina limitních příkladů se řeší přechodem na funkce, často se používá l'Hospitalovo pravidlo. Tohle se nicméně občas pokazí hned na začátku, když nejde přejít k funkcím. Typickým příkladem jsou mocniny se záporným základem jako (−2)ⁿ, také faktoriál n!, kde vlastně nevíme, jak jej změnit ve funkci (i když to se dá udělat, viz funkce Gama) a jak derivovat. Je tedy třeba zkusit alternativní přístup, srovnání často pomůže.

Příklad: Dokážeme, že

Protože tento podíl je kladný a my se snažíme ukázat, že jde k nule, použijeme na to jednostranné srovnání a zkusíme najít vhodný horní odhad. Všimněte si, že hledáme limitu, a proto nám záleží pouze na velkých n a proto můžeme předpokládat, že n > 3, a tak si ušetřit problémy se značením. Pak dostaneme

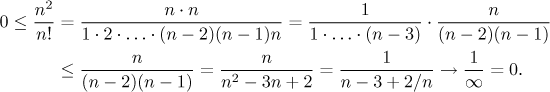
Podle druhého jednostranného srovnání nahoře konverguje daná posloupnost k nule, přesně jak jsme tvrdili. Všimněte si, že když jsme v posledním kroku výpočtu nacházeli limitu, použili jsme k tomu krácení n ve zlomku. Také tento příklad byl typický pro šuplík polynomy a podíly s mocninami.

Důvod 3. Někdy i máme rozumnou alternativu, ale zvolíme srovnání, protože je to jednodudšší a kratší. Například pomocí l'Hospitalova pravidla či vytknutí hravě spočítáme, že

Srovnání to nicméně udělá ještě rychleji:

Použití srovnání probíhá ve dvou krocích:

Krok 1. Najdeme nějaké(á) srovnání (tj. odhady) pro danou posloupnost. Oscilující ale omezené výrazy mají přirozené odhady, kterých můžeme použít k algebraickému nalezení odhadů pro celou posloupnost. Často také najdeme odhady ignorováním určitých částí posloupnosti (viz poslední příklad).

Krok 2. Najdeme limitu odhadu (odhadů). Pak se podíváme, jestli je možné udělat nějaký závěr pomocí některého z výše citovaných srovnávacích tvrzení. Pamatujme, že Věta o sevření vyžaduje, aby oba odhady konvergovaly k témuž číslu.

Poznámka: Výše citovaná tvrzení mají velice užitečný důsledek, který lze používat jako nástroj (tvrzení), dá se vyjádřit několika způsoby.

Když se omezená posloupnost vynásobí posloupností konvergující k nule, dostaneme posloupnost konvergující k nule.
Když se omezená posloupnost vydělí posloupností konvergující k nekonečnu, dostaneme posloupnost konvergující k nule.

Použití srovnání není tak přímočaré jako ostatní metody v jednom důležitém aspektu: pro ostatní metody jsme měli typické příklady, na které se používají. Zde takový typ není (pokud nepočítáme oscilující výrazy). Hodně záleží na zkušenosti a intuici.

Poznámka: Ta dvě jednostranná tvrzení na začátku jsou velmi blízce spojeny, je to vlastně tentýž problém a tentýž výsledek. Ukázat, že nějaká posloupnost konverguje do nekonečna, je ekvivalentní problému ukázat, že její reciproká hodnota (jedna lomeno tato poslooupnost) konverguje k nule. A když přecházíme k reciprokému problému, nerovnosti se prohodí. Například u posledního příkladu jsme mohli ekvivalentně ukázat

pomocí téhož triku, jen položeného opačně:

V části Řešené příklady - Limita jsou tyto metody použity v tomto příkladě, tomto příkladě a tomto příkladě.

Další šuplík: polynomy, sumy a podíly s mocninami
Zpět na Přehled metod - Limita