Šuplík "neurčitý součin"

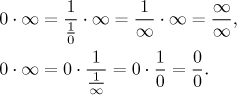
Zde se podíváme na následující problém: Potřebijeme najít limitu součinu a_n⋅b_n a při pokusu o dosazení nekonečna jsme zjistili, že tento součin je typu ∞⋅0.

Standardním řešením je algebraická transformace součinu v podíl. Pokud to uděláme, jak je ukázáno níže, tento podíl bude neurčitého typu a dá se použít l'Hospitalovo pravidlo (viz šuplík "neurčitý podíl").

Jak změníme součin v podíl? Vybereme si jeden činitel ze součinu aa plikujeme na něj trik "děleno děleno"; víme totiž z algebry, že pro každé nenulové A máme 1/(1/A) = A. Výsledný zlomek bude typu, který záleží na tom, kterou část součinu takto upravíme, zda to byla ta "nula" nebo to "nekonečno":

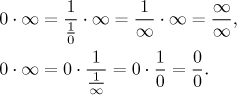
Všimněte si, že jsme vlastně podváděli, když jsme napsali 1/0 = ∞. Víme, že když dělíme nulou, musíme zkontrolovat její typ, pouze potom je možné udělat nějaké závěry. Protože 1/0 = ∞ (či mínus nekonečno) pouze pokud je 0 jednostranná, vyplývá z toho, že pokud není nula v neurčitém součinu jednostranného typu, nemůžeme ji "dát dolů". Co potom? Jedna z možností je použít tu alternativu, kde dáváme "dolů" tu nekonečnou část.

Co kdyby to nefungovalo? Další možností je nejprve vyřešit příklad, ve kterém je ta "nula" v absolutní hodnotě, pak začít přemýšlet o znaménku. Další detaily jsou zde.

Ve většině příkladů se ale tento problém nevyskytuje.

Příklad:

Dostali jsme neurčitý součin, takž jej změníme ve zlomek. Kterou část si k tomu vybereme? n vypadá jednoduše, tak to s ním zkusíme. A protože budeme používat l'Hospitalovo pravidlo, přejdeme od posloupností k funkcím.

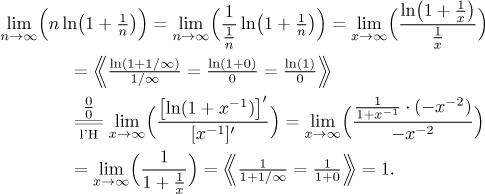
Co by se stalo, kdybychom si zkusili hrát z druhou částí součinu?

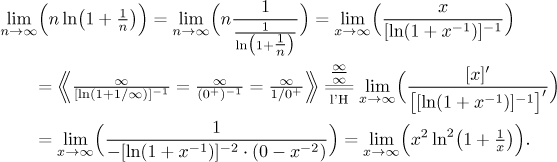
Jak vidíte, nový výraz je ještě horší než ten původní, takže takto to nepůjde.

Poznámka k 0⁺: Když jsme dali nulu do jmenovatele, museli jsme zkontrolovat, zda je jednostranná (viz poznámka výše). Víme, že ln(1 + 1/n)→0; navíc pro kladné n máme 1 + 1/n > 1, takže také ln(1 + 1/n) > 0. Z toho plyne, že ln(1 + 1/n)→0⁺, přesně jak jsme ve výpočtu tvrdili.

Volba části, kterou transformujeme, rozhoduje o úspěchu výpočtu. Obvykle "dáváme dolů" část, která se touto transformací příliš nezkomplikuje. Typicky to jsou mocniny, protože u těch se jen změní znaménko exponentu: n^a = 1/n^−a, a také exponenciály: eⁿ = 1/e⁻ⁿ. Tyto výrazy se nezhorší, když se zderivují. Na druhou stranu, když jsme "dali dolů" logaritmus, stal se komplikovanější a derivace to ještě zhoršila. S trochou zkušenosti byste měli být schopni odhadnout, kterou část použít v transformaci. Přinejhorším se dají vždycky zkusit oba způsoby a jeden by měl zabrat.

V části Řešené příklady - Limita jsou tyto metody použity v tomto příkladě, tomto příkladě, a tomto příkladě.

Další šuplík: neurčitý rozdíl
Zpět na Přehled metod - Limita