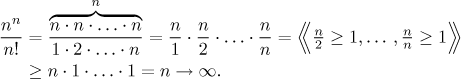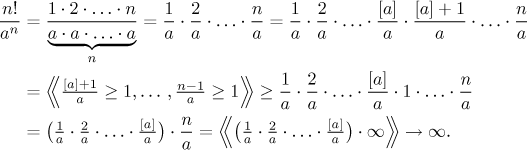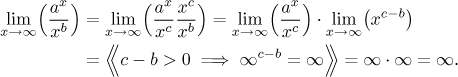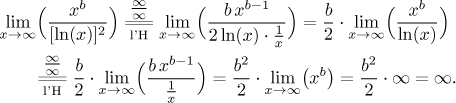Řád nekonečna

Když mluvíme o rozličných "velikostech" nekonečna, mluvíme vlastně o "řádu". To je matematický pojem týkající se srovnání, jak malé či velké funkce jsou v určitém bodě. Protože to potřebujeme pouze pro posloupnosti, nepokryjeme to zcela obecně a budeme méně formální. Snad to tak bude srozumitelnější.

Uvažujme dvě posloupnosti, a_n a b_n. Chceme porovnat, jak se chovají, když se n stane opravdu velkým. Typicky by obě posloupnosti šli do nekonečna a my bychom potřebovali porovnat "velikosti" těchto nekonečen, ale není to jediná možnost. Můžeme také porovnávat, jak posloupnosti konvergují k určitému číslu. Typickým příkladem je, když obě konvergují k nule. Víme, že 0/0 je neurčitý výraz, takže nás může zajímat, která z těch dvou nul je "víc nula" a vyhraje. Pro příklady tohoto chování se podívejte na část 0/0 pojednání o neurčitých výrazech.

Budeme vlastně mluvit o dvou typech srovnání. Pojem řádu srovnává nekonečna přibližně; když má jeden výraz vyšší řád, znamená to, že je podstatně větčí, ne jen o trochu. Z jiného pohledu se dá říst, že když jsou dvě posloupnosti stejného řádu v nekonečnu, pak jsou zhruba stejné.

To se hodí, když zjišťujeme, které části jsou méně důležité a které části převáží nad kterými když dojde na přímou konfrontaci, ale není to dostatečné pro přesný odhad limity. Jak například uvidíme později, 2n a 5n mají stejný řád, ale když je vydělíme n ve zlomku, dají v nekonečnu rozdílné limity (2 oproti 5).

Představíme proto další srovnání. Nemá formální název, protože nebývá formálně zavedeno v učebnicích, takže jen budeme říkat, že se dvě posloupnosti "chovají v nekonečnu stejně", a používat značení ∼.

Definice.
Uvažujme posloupnosti {a_n} a {b_n}.
Řekneme, že a_n má (v nekonečnu) vyšší řád než b_n, značeno b_n = o(a_n), jestliže

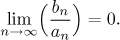
Řekneme, že tyto dvě posloupnosti jsou (v nekonečnu) stejného řádu, jestliže existuje kladné číslo A splňující

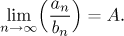
Řekneme, že tyto dvě posloupnosti se v nekonečnu chovají stejně, značeno a_n ∼ b_n, jestliže

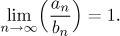
Všimněte si, že b_n = o(a_n) lze také ekvivalentně definovat podmínkou

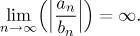
(Absolutní hodnotu jsem museli použít, protože 1/0 nemusí mít limitu či může jít k plus/mínus nekonečnu, zatímco 1/|0| = ∞.)

Jaké mají tyto pojmy použití? Řád nám umožňuje získat intuitivní pochopení rychlosti růstu, soustředí se na podstatné a ignoruje méně důležité faktory. Je například snadné ověřit z definice, že n² má vyšší řád než n. Je stejně snadné ověřit, že 135n má stejný řád jako n. Proč by tomu tak mělo být? Důvod je jednoduchý. Víme ze zkušenosti, že n² dává mnohem větší výsledky než n po dosazení velkých čísel n. Teď si představme velký násobek n, například 1000000n. Pokud za n dosadíme menší čísla, tak 1000000n bude větší než n². Jak ale dosazujeme větší a větší čísla, dříve či později výraz n² vyhraje nad 1000000n, čímž myslíme, že bude dávat mnohem větší výsledky, větší o kolik chceme. Toto platí pro všechny výrazy A⋅n. To je také význam řádu: zajímá jej pouze srovnání v nekonečnu. Všechny výrazy formy A⋅n jdou řádu n, protože jestliže A⋅n přebije nějaký výraz v nekonečnu, pak jej přebije i n, a jestliže je A⋅n přebito určitým výrazem, pak to platí i pro n.

Řád tak rozděluje výrazy do skupin, uvnitř každé skupiny mohou být další srovnání (2n určitě roste do nekonečna rychleji než jen n), ale rozdíl není tak velký; důležité je, že libovolný člen jedné skupiny přebije libovolného člena další skupiny, pokud tato má nižší řád. Obvykle si vybíráme ten nejjednodušší člen jako reprezentanta celé skupiny, či "typu", jak také říkáme, například výrazy jako 2n, −3n, (n − 5), (n² + 13)/n jsou všechny typu (řádu) n.

Nejpopulárnější typy jsou representovány mocninami, eponenciálami,mocninami logaritmů, faktoriály a obecnými mocninami. Přímá aplikace řádu umožňuje rychle určit limitu podílu těchto typů, pokud tedy dokážeme ustanovit nějaké obecné srovnání.

Největší užitek je nicméně z kombinace řádu a vztahu "chovají se stejně". Zatímco řád je příliš hrubý na správné určení limity, pokud se dvě posloupnosti chovají stejně, musí mít stejnou limitu v nekonečnu. To nám umožňuje nahradit komplikované výrazy jednoduššími, které se chovají stejně, což ulehčí následnou práci. Nejpřirozenější způsob vytváření těch jednodušších výrazů je pomocí řádu: všechny části výrazu, které jsou nižšího řádu, lze často ignorovat. Mluvili jsme o tom v sekci Intuitivní výpočty v části Teorie - Limita. Teď je čas pro trochu přesnosti.

Fakt.
Jestliže a_n→L a a_n ∼ b_n, pak b_n→L.

Toto ukazuje hlavní přínos srovnání. Teď přesně vyjádříme, jak zjednodušovat posloupnosti.

Fakt.
Jestliže b_n = o(a_n), pak (a_n + b_n) ∼ a_n.

Řečeno slovy, když hledáme limitu nějakého součtu, můžeme ignorovat části nižšího řádu, aniž bychom udělali chybu. Důkaz je vlastně velice snadný. Máme dokázat, že podíl (a_n + b_n)/a_n konverguje k 1. Vydělíme zlomek a dostaneme (1 + b_n/a_n). Protože se předpokládá, že a_n je vyššího řádu než b_n, podíl v závorce konverguje k nule a proto celý výraz konverguje k 1, přesně jak to potřebujeme.

Když se pořádně dokážou tyto dva fakty spolu se škálou mocnin, tak se intuitivní výpočet, o kterém jsme se už zmiňovali, stane správnou a korektní matematickou metodou, není už pak třeba dále dokazovat jím získané závěry! Bohužel, jak už jsme poznamenali, tato teorie nebývá pokryta (snad žádnou) učebnicí kalkulu, takže se na ni nebudeme spoléhat ani v Math Tutoru; budeme ji jen používat jako pomocnou metodu a potvrzovat získané výsledky obvyklejšími metodami (jako ten vytýkací trik). To neznamená, že byste to nemohli zkoušet ve škole, ale než začnete odevzdávat písemky s výsledky odůvodněnými větami typu "exponenciály přebijí logaritmy", ujistěte se, že tomuto tématu dobře rozumíte; zkoušející budou mít k vašemu postupu určitě otázky a jestli nebudete umět odpovědět...

Jak už jsme zmínili, mocniny a podobné výrazy jsou nejpopulárnějš typy, které bývají srovnávány, i když typů existuje samozřejmě víc; ty jsou ovšem vzácnější. V sekci Intuitivní výpočty v části Teorie - Limita jsme ustanovili škálu mocnin; ve skutečnosti jsme tvrdili následující:

   n! = o(nⁿ),
   aⁿ = o(n!) pro všechna a s |a| > 1,
   n^b = o(aⁿ) pro všechna |a| > 1, b > 0,
   [ln(n)]^c = o(n^b) pro všechna b > 0, c > 0.

To vše se dá dokázat, něco pomocí l'Hospitalova pravidla, jiné srovnáním (viz Apendix níže). Tvrdili jsme také, že v každé kategorii mají výrazy s větší konstantou vyšší řád:

   Jestliže |a| > |b| > 1, pak bⁿ = o(aⁿ),
   Jestliže a > b > 0, pak n^b = o(n^a),
   Jestliže a > b > 0, pak [ln(n)]^b =; o([ln(n)]^a).

Zde jsou důkazy velice snadné, když si napíšete příslušný podíl k důkazu určitého vztahu, uvidíte, že se pěkně pokrátí.

Jedna zajímavá věc ohledně řádu je, že z něj vznikají zajímavé relace. Jmenovitě relace "být stejného řádu" je ekvivalence a relace "být většího řádu" je tranzitivní. To mimo jiné znamená, že jakmile dokážeme výše vypsaná fakta o mocninách, exponenciálách atd., můžeme automaticky používat další srovnání přes prostředníka; například automaticky máme, že ln(n) = o(n!).

Vlastně bychom mohli udělat stejné úvahy pro dvě funkce f (x) a g(x) definované na nějakém intervalu (K,∞), a zajímat se o to, jak se srovnají, když se x stává velkým. Všechno by fungovalo stejně, konec konců, jak už jsme poznamenali na začátku, pojem řádu je velmi obecný. Podíváme se na to blíže při zkoumání funkcí, viz řád funkcí v části Funkce - Teorie - Limita.

Tvrzení n! = o(nⁿ): Toto se nejlépe dokáže pomocí jednostranného srovnání a chytrého rozřazení podílu.

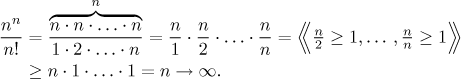
Tvrzení aⁿ = o(n!) pro a > 1: To se dokazuje podobně jako předchozí případ. Symbolem [a] značíme celou část a, tj. největší celé číslo, které je menší či rovno číslu a.

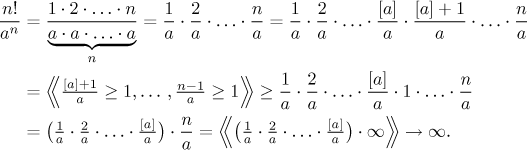
Tvrzení n^b = o(aⁿ) pro a > 1: Toto se dokazuje přechodem na funkce a l'Hospitalovým pravidlem. Začne se případem b = 1:

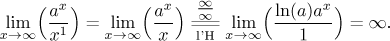
Jestliže je b kladné celé číslo, pak se důkaz dělá opakováním l'Hospitalova pravidla b-krát. Formálně se to nejlépe zvládne indukcí, udělali už jsme b = 1, teď to uděláme pro přirozené číslo b předpokládaje, že už jsme to dokázali pro b − 1:

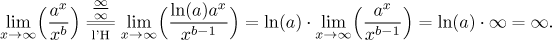
Jestliže b > 0 není celé číslo, uvažujme nějaké celé číslo c větší než b. Pak (c − b) > 0, a proto

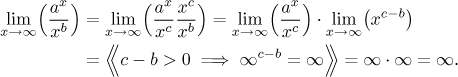
Tvrzení [ln(n)]^c = o(n^b): To se také dělá pomocí l'Hospitalova pravidla. Postup je podobný důkazu předchozího tvrzení, dělá se ve třech krocích. Ukážeme jen, jak by se dokazoval případ c = 2; to se musí l'Hospital použít dvakrát.
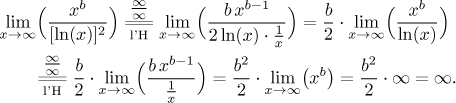