Zde se podíváme na trochu teorie ohledně konvexity. Pro praktický přístup pomocí derivací viz Konvexita v části Derivace - Teorie - Průběh funkce.
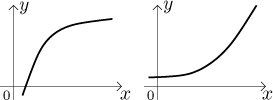
Uvažujme funkci rostoucí na intervalu. To nám říká, že funkce roste, ale neříká to jak, protože je mnoho způsobů, kterým může funkce růst. Z těchto mnoha jsme vybrali dva nejhezčí a v jistém smyslu nejtypičtější.

Rozdíl je podstatný ze dvou důvodů. První je, že funkce jsou užitečné, mají popisovat věci. Zde víme, že určitá kvantita roste, ale v prvním obrázku máme trend, kdy se růst zpomaluje, zatímco na druhém se zdá, že se růst trochu vymkl z ruky. V závislosti na situaci může být jeden z těchto případů velmi špatný a druhý velmi dobrý. Pokud například graf ukazuje, kolik máme v důchodovém fondu, pak by ten druhý obrázek byl velmi příznivý (a často se objevuje v reklamě), úroky se během let pěkně načítají. Na druhou stranu, pokud graf ukazuje, kolik tepla generuje určitá reakce, kterou mícháte v laboratoři, pak ten první obrázek je něco, co byste měli rádi. Druhý obrázek se obvykle nazývá "exploze" a měli byste rychle zmizet co nejdál.
Pro studenta kalkulu je asi důležitější druhý význam, protože tyto dva tvary jsou velmi odlišné když dojde na kreslení grafu; první se "stáčí dolů" a druhý se "stáčí nahoru". Tyto dva trendy jsou ve skutečnosti nezávislé na růstu funkce, na následujícím obrázku se první dva grafy "stáčí dolů" (jeden je klesající, druhý není monotonní a rostoucí už jsme viděli nahoře), pak máme dva grafy, které se "stáčí nahoru" (zase jeden klesající, jeden nemonotonní a rostoucím jsme začali).

Matematicky, pokud se graf někde "stáčí nahoru", nazývá se konvexní, když se někde "stáčí dolů", nazývá se konkávní. Když se o toto zajímáme, řekneme, že sledujeme konvexitu dané funkce, ale toto není příliš rozšířené jméno a většina autorů nemá jedno souhrnné jméno pro konvexitu/konkávitu.
Život je pes a jsou funkce, které jsou pěkně divoké co se týče konvexity, klidně si mění způsob, kterým jdou, úplně všude a nejde udělat rozumný obrázek (viz Dirichletova funkce). Pro typickou funkci má nicméně graf části, na kterých se vždy drží jednoho z těchto tvarů, takže je chvíli konvexní (na intervalu), pak konkávní, pak... To je přesně ta situace, na kterou se teď podíváme. Tento pojem je vlastně svou povahou docela podobný monotonii (jak za chvíli uvidíte), takže bychom měli začít konvexitou v bodě. Ve skutečnosti tohle ale prakticky nikdo nepoužívá, takže to necháme jako poznámku na konec a rovnou se vrhneme na konkávitu na množině (typicky na intervalu).
Jak vyjádříme matematicky, že se funkce "stáčí nahoru" jako na úplně prvním obrázku? Jsou dva způsoby, jak se na to dívat. První je, že když jdete z jednoho bodu do druhého a pak zkusíte ještě jeden krok, musíte jít víc do kopce. Druhý úhel pohledu je, že když se zkusíte pohnout z nějakého bodu, tak čím dál chcete jít, tím větší sklon nahoru vás čeká. A to by samozřejmě mělo být pravda na všech částech křivky.
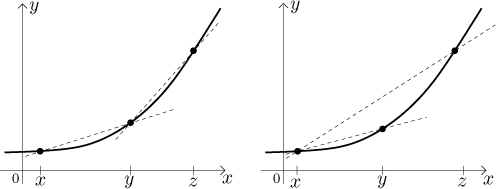
Ten sklon, o kterém mluvíme, jsou vlastně směrnice přímek spojujících zmíněné body, takže to, co jsme teď řekli, se přeloží v nerovnosti mezi směrnicemi. Ty se snadno najdou a dostaneme následující definici.
Definice (konvexita).
Nechť f je funkce definovaná na množině M.
Řekneme, že f je konvexní na M, jestliže pro libovolné tři bodyx < y < z∈M platí
Ekvivalentně, f je konvexní na M, jestliže pro libovolné tři body
x < y < z∈M platí
Řekneme, že f je konkávní na M, jestliže pro libovolné tři body
x < y < z∈M platí
Ekvivalentně, f je konkávní na M, jestliže pro libovolné tři body
x < y < z∈M platí
Řekneme, že bod
x∈D( f ) je inflexní bod nebo bod inflexe, jestliže existuje levé okolí bodu x, na kterém je f konvexní, a pravé okolí bodu x, na kterém je f konkávní, nebo jestli existuje levé okolí bodu x, na kterém je f konkávní, a pravé okolí bodu x, na kterém je f konvexní.
Krátce, inflexní body jsou ty, ve kterých se mění konvexita. Jako obvykle nejčastěji zkoumáme konvexitu na intervalech, mimo jiné protože pak na to máme skvělé nástroje.
Příklad:
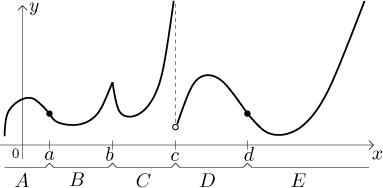
Funkce na obrázku je konvexní na intervalech B, C a E, konkávní na intervalech A a D a má inflexní body a a d (mění také konvexitu v c, ale tento bod není v definičním oboru f ).
Než se pustíme dále, uvedeme větu, která říká, že ten obrázek nahoře nebyl přehnaně pěkný, že jakmile má funkce nějakou konvexitu, nemůže už strašit nepříjemnými skoky jako u monotonie.
Věta.
Jestliže je funkce konvexní na daném otevřeném intervalu či je na něm konkávní, pak je tam i spojitá.
Jsou alternativní způsoby, jak nahlížet na (a definovat) konvexitu; měly by vypadat přirozeně, když se podíváte na obrázky.
Začneme s první nerovností ve formální definici, která popisovala konvexitu pomocí dvou následných směrnic. Trochu algebry ji přepíše takto:
![]()
To vypadá docela hnusně, ale začne to být zajímavé v okamžiku, kdy si uvědomíme následující. Uvažujme tento vzorec (s čísly x,z pevně zvolenými a proměnnou t):
![]()
Je to vlastně vzorec pro přímku spojující body
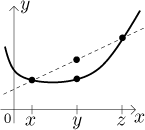
Geometricky říkáme toto: Zvolíme dva body, x a z. Pak si zvolíme nějaký bod mezi nimi a hodnota f v tomto bodě musí být menší než či rovna hodnotě, kterou bychom dostali spojením těch dvou zvolených bodů úsečkou. Tím dostáváme následující geometricou definici konvexity, a protože budeme vybírat pouze dva body, přejmenujeme z na y:
Funkce je konvexní na intervalu I, jestliže pro libovolné dva body
Funkce je konkávní na intervalu I, jestliže pro libovolné dva body
Tento geometrický pohled na konvexitu lze vyjádřit ještě jiným způsobem.
Matematici dobře vědí, že když jsou x a y dvě reálná čísla, pak
všechna čísla mezi nimi lze vyjádřit jako
Funkce je konvexní na intervalu I, jestliže pro libovolné dva body
![]()
Funkce je konkávní na intervalu I, jestliže pro libovolné dva body
![]()
Poslední geometrická charakterizace konvexity není univerzální jako ty výše, protože nefunguje pro některé funkce. Důvodem je, že ne každý graf funkce je dostatečně pěkný na to, aby měl tečny (viz tečny v části Derivace - Teorie - Aplikace). Předpokládejme tedy na chvíli, že máme funkci, jejíž graf je tak pěkný, že má všude tečny.

Funkce je konvexní na nějakém intervalu přesně tehdy, jestliže kdykoliv
nakreslíme tečnu ke grafu v nějakém bodě tohoto intervalu, pak graf (přesněji
jeho část odpovídající tomuto intervalu konvexity) leží na nebo nad touto
tečnou.
Funkce je konkávní na nějakém intervalu přesně tehdy, jestliže kdykoliv
nakreslíme tečnu ke grafu v nějakém bodě tohoto intervalu, pak část grafu
odpovídající tomuto intervalu konkávity leží na nebo pod touto tečnou.
Inflexní bod je charakterizován tím, že když nakreslíme tečnu v tomto bodě,
pak existuje takové okolí, že odpovídající část grafu leží na jedné straně
od tohoto bodu nad tečnou a na druhé straně pod tečnou.
Další možná charakterizace vypadá takto: Jestliže uvažujeme rovinnou oblast nad grafem funkce, pak je tento útvar konvexní přesně tehdy, je-li funkce konvexní.
Poznámka: Můžeme také definovat ryzí konvexitu tak, že by se všechny předchozí nerovnosti změnily v ostré. To je možné, ale moc se to nepoužívá. Jeden z důvodu, proč bychom to mohli chtít, je, že někteří lidé jsou trochu nesví z toho, že existují funkce, které jsou na jednom intervalu zároveň konvexní a konkávní. Jsou to přesně všechny lineární funkce neboli přímky.
Spojování intervalů.
Zde se podíváme na následující situaci: Víme, že určitá funkce
f má určitou konvexitu na daných dvou intervalech I a J.
Můžeme říct něco o její konkávitě na sjednocení? Bohužel moc ne, zde je
situace o dost horší než s monotonií. Podívejme se třeba na ten příklad s
písmeny A, B, C,... Měli jsme tam funkci, která byla
konvexní na intervalech B a C, ale není konvexní na jejich
sjednocení, i když se tam graf krásně napojuje, bez skoků. Existují určité
podmínky, které lze ověřovat, ale nejsou příliš pěkné a neexistuje pohodlný
postup.
Vlastně jediný případ, kdy lze pro funkci konvexní na dvou intervalech bez dalšího zkoumání zaručit konvexitu na sjednocení, je ten, když se ony dva intervaly překrývají víc než jediným bodem. Bohužel, taková situace prakticky nenastává u aplikací.
Zde uděláme zřejmé, definujeme lokální konvexitu. Globální vlastnost by měla být dostatečnou inspirací. Abychom ujasnili, co máme na mysli, ukážeme několik obrázků funkcí, které jsou konkávní v daném bodě.

Definice (lokální konkávita).
Nechť f je funkce definovaná na nějakém okolí bodu a.
Řekneme, že f je konvexní v a, jestliže existuje okolí U bodu a takové, že pro libovolné dva body x,y zU ∩ D( f ) splňujícíx < a < y platí
Řekneme, že f je konkávní v a, jestliže existuje okolí U bodu a takové, že pro libovolné dva body x,y z
U ∩ D( f ) splňujícíx < a < y platí
Jak se dá čekat, funkce je konvexní na otevřeném intervalu přesně tehdy, je-li konvexní ve všech jeho bodech, obdobné tvrzení platí o konkávitě. Protože většina učebnic se ani nenamáhá tento pojem zavést, budeme jej také ignorovat, toto je jediná chvíle, kdy o něm v Math Tutoru uslyšíte.