Příklad: Určete definiční obor následující funkce:

Řešení: Nejsou tam obecné mocniny, které bychom museli přepsat, takže hledáme problémy ve funkci tak, jak byla zadána. Začneme zleva:

1. Arcsin vyžaduje, aby jeho argument byl z intervalu ⟨−1,1⟩, máme tedy podmínku

2. V arcsinu je zlomek, jmenovatel nesmí být nulový, takže dostaneme x ≠ 0.

3. Pak je tam odmocnina, její argument musí být kladný či nulový:

4. Logaritmus vyžaduje, aby byl jeho argument kladný:

5. Zlomek v logaritmu potřebuje nenulový jmenovatel: (x + 1) ≠ 0. Dostáváme x ≠ −1.

6. Třetí člen potřebuje nenulový jmenovatel: sinh(x + 2) ≠ 0.

7. Nakonec se dostáváme k logaritmu napravo, jeho argument musí být kladný:

Pak máme v logaritmu odmocninu, ale její argument x² + 12 je vždy alespoň 12, takže určitě nikdy nedostaneme záporná čísla a nevyplývá z toho žádné omezení. Protože polynomy a sinh přijmou libovolný argument, další podmínky již nejsou.

Teď je třeba určit množiny, které odpovídají jednotlivým podmínkám. podmíneky 2 a 5 už není třeba nic dělat, na ostatní se podíváme.

Podmínka 1: Takovéto dvojité nerovnosti lze řešit dvěma způsoby. Jeden je řešit každou nerovnost zvlášť, což se dělá nejlépe tak, že se přepíší na typ "nějaký součin/podíl lineárních faktorů srovnávaný s nulou". Výsledné množiny se pak protnou, protože potřebujeme, aby obě nerovnosti platily zároveň. Tuto metodu necháváme čtenáři, protože ji také použijeme u podmínky 3, kde ji už ukážeme. Pokud to opravdu potřebujete vidět, klikněte sem.

Zde raději ukážeme metodu alternativní, protože tu již v dalších podmínkách neukážeme. Vynásobíme dvojitou nerovnost jmenovatelem, abychom se zbavili zlomků. Na to ale potřebujeme vědět, jaké má jmenovatel znaménko, protože v záporném případě musíme změnit směry nerovností. Protože znaménko může být libovolné, musíme rozdělit reálnou osu na dvě části, jednu, kde je jmenovatel kladný, a druhou, kde je záporný, a řešíme problém v každé části zvlášť. Řešení každé části je ale platné pouze tam, kde jsme řešili, takže cokoliv mimo se musí ignorovat.

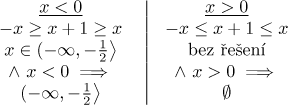
Protože máme volbu, zda bude jmenovatel kladný či záporný, dostaneme konečnou odpověď sjednocením částečných výsledků. Druhá podmínka tedy znamená

Podmínka 3: Když povýšíme obě strany rovnice na e a zkrátíme nalevo e^ln, dostaneme

Dá se to také určit pomocí znalosti grafu logaritmu.

Tento typ nerovnosti se nejlépe řeší tak, že se na jedné straně vyrobí nula a to, co vznikne na druhé, se rozloží na lineární faktory.

Dělící body pro znaménka faktorů jsou −3, −1, 1, takže se reálná osa rozpadne na čtyři intervaly, pro každý z nich určíme znaménko.

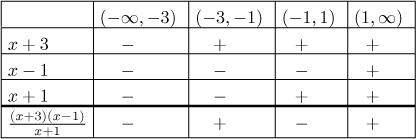
Takže druhý a čtvrtý interval fungují pro danou nerovnost. Dále se potřebujeme podívat na dělící body, dosadíme je do výrazu nalevo a ověříme, který z nich vyhovuje dané nerovnici. Body −3 a 1 jsou v pořádku, zatímco −1 nefunguje. Závěr: Podmínka 3 říká

Podmínka 4: Vidíme, že tato podmínka je vlastně méně omezující než podmínka zkoumaná v Podmínce 3, a protože budeme výsledký pronikat, tyto dvě podmínky dají stejně zase výsledek Podmínky 3. Nemusíme tedy tuto řešit.

Podmínka 6: Mohlo by se stát, že bude hyperbolický sinus roven nule? Ano, pokud je jeho argument nulový. Tato podmínka tedy vlastně říká x + 2 ≠ 0, neboli x ≠ −2.

Podmínka 7: Tohle je vlastně docela těžké. Máme nerovnost s odmocninou, takže první instinkt může být přesunout "2x" napravo a umocnit. Bohužel, umocňování nerovností nefunguje, pokud nevíme něco o znaménkách a navrch ještě nemáme trochu štěstí. Zde jsou dva případy. Jestliže x > 0, pak je 2x kladné, měli bychom tedy nerovnost, kde jsou obě strany kladné (odmocnina je vždy kladná) a můžeme umocnit. Jestliže ale x < 0, pak mají strany nerovnice rozdílná znaménka a nelze umocnit. To ukazuje, že nemáme štěstí.

Nejsnažší metoda tedy asi bude skrz nulové body. Začneme tím, že vyřešíme rovnici namísto nerovnice:

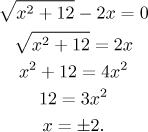
Protože umocňování rovnice není ekvivalentní operace, můžeme dostat "falešné kořeny", takže nejprve tato dvě čísla ověříme. Po dosazení do původní (neumocněné) rovnice zjistíme, že x = 2 je opravdu řešení, zatímco −2 není a vypustíme jej. Máme jeden nulový bod, takže se reálná osa rozpadne na dva intervaly s konstantním znaménkem, obě znaménka dostaneme dosazením nějakých pěkných čísel (například 0 a 3) do výrazu:

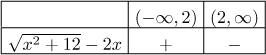
Vidíme, že první interval je oblast, kde je nerovnost splněna, zbývá zjistit, jestli má být uzavřený nebo otevřený. To se udělá hravě dosazením dělícího bodu 2 do nerovnosti, vidíme, že nefunguje. Podmínka 7 tedy znamená

x∈(−∞,2).

Teď potřebujeme proniknout všechny podmínky:

Řešení je

D( f ) = ⟨−3,−2) ∪ (−2,−1).

Další příklad
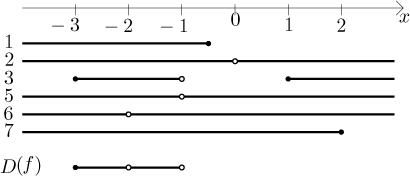
Zpět na Řešené příklady - Reálné funkce