Příklad: Určete symetrii následující funkce:

Řešení: Nejprve určíme definiční obor. Jsou dva zdroje problémů. Jeden je domocnina, ale výraz pod ní splňuje x² + 1 ≥ 1 > 0, takže tam problém není.

Další na řadě je logaritmus. Jeho argument musí být kladný, což dá trochu víc práce. "Standardní" přístup by byl najít nulové body tohoto výrazu a určit znaménka (viz také tento řešený příklad). V tomto případě nejsou nulové body, takže tento výraz je buď vždy kladný, nebo vždy záporný. Zkusíme dosadit x = 0 a vidíme, že platí to první a proto není žádné omezení na definiční obor. Jde to i jinak: Protože x² + 1 > x², tak je ta odmocnina vždy větší než |x|, proto když k ní přičteme x, určitě dostaneme něco kladného. Další dva způsoby, jak na to jít, přidáme v poznámce na konci.

Každopádně vidíme, že tato funkce má jako defiiční obor celou reálnou osu, a protože jde o symetrickou množinu, je zde šance na symetrii funkce. Zkusíme obvyklý postup, dosadíme (−x) za x.

Teď máme trochu problém. Zdá se, že není možné to mínus vytáhnout ven nebo zrušit, takže tato funkce možná ani není vůbec symetrická. Takovéto "pocity" se ale mohou mýlit a my musíme rozhodnout najisto. Nejlepší řešení situace je tedy zkusit ověřit oba druhy symetrie pomocí rovnic. Nejprve zkusíme, za funkce není sudá, logaritmů se zbavíme tak, že povýšíme obě strany rovnice na exponenciálu a zkrátíme "e^ln":

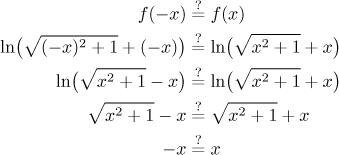
Máme rovnici, která není pravdivá pro všechna x z definičního oboru (tedy pro všechna reálná x), původní rovnost tedy neplatí a funkce není sudá. Teď zkusíme lichost. Abychom mohli použít krácení "e^ln", musíme zařídit, aby byl na pravé straně logaritmus vnější funkcí.

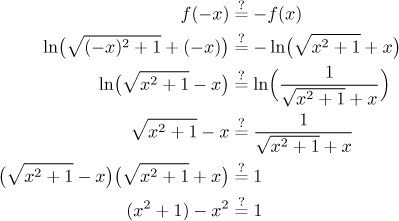
Teď jsme dostali rovnost, která platí pro všechna reálná x, takže jsme právě překvapivě dokázali, že tato funkce je lichá.

Když už teď víme, že výpočty používají sdružený člen "odmocnina mínus x", umíme to dokázat přímo:

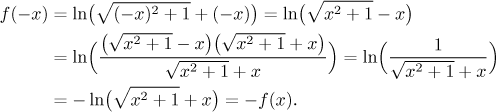
Funkce je tedy opravdu lichá.

Poznámka: Zde ukážeme další dva způsoby, jak dokázat, že výraz "odmocnina plus x" je vždy kladný.

Jedna možná argumentace je takto: Jsou dva případy. Jestliže je x kladné, pak celý výraz je evidentně kladný. Jestliže x = 0, pak dosazení do výrazu dá 1, což je určitě kladné. Co když je x záporné? Pak je člen "odmocnina mínus x" určitě kladný, takže můžeme tímto členem vynásobit žádanou nerovnost bez změny směru nerovnosti:

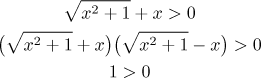
Dostali jsme pravdivou nerovnost a operace byly ekvivalentní, takže platí i původní nerovnost, tedy zkoumaný člen je kladný pro x < 0.

Druhá alternativa je tato: Mohlo by nás to svádět k převodu x na druhou stranu nerovnice

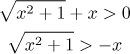
a pak se zbavit té otravné odmocniny umocněním obou stran nerovnice. Bohužel, tato operace nefunguje obecně. Funguje jen tehdy, pokud víme, že znaménka na obou stranách jsou kladná. Je také možné umocnin obě strany rovnice, pokud jsou obě záporné, ale pak se musí změnit směr nerovnosti. Krátce a stručně, umocňování nerovností je riskantní a je dobré se tomu vyhýbat.

Jestli si ale v matice věříte, je možné to zkusit a dostat kratší řešení. Co můžeme říct o znaménkách obou stran rovnice? Levá strana je vždy kladný, takže umocnit můžeme jen tehdy, je-li pravá strana také kladná, neboli pro -x > 0. Umocnit tedy můžeme jen pro x < 0, ale naštěstí pro nás je to právě ten netriviální případ, protože jak už jsme viděli, pro x kladné či nulové žádaná nerovnost evidentně platí. Budeme tedy předpokládat, že x < 0, a umocníme:

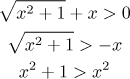
Zase jsme dostali nerovnost, která vždy platí, což je další potvrzení, že ten logaritmus má smysl pro všechna x.

Další příklad
Zpět na Řešené příklady - Reálné funkce