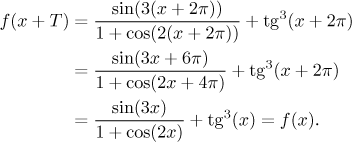Příklad: Určete periodicitu následující funkce:

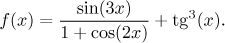
Řešení: Vždy začínáme určením definičního oboru. Zde máme dva problémy. Nejprve tangens vyloučí všechna čísla typu π/2 + kπ. Máme také zlomek, jmenovatel nesmí být nula. Proto kosinus nemůže být −1, tedy čísla (2x) nemohou být (2k + 1)π, neboli x nemůže být π/2 + kπ. Úžasnou náhodou je tato podmínka stejná jako ta první, to je ale klika. Definiční obor je tedy všechna reálná čísla bez těch vypsaných výše.

Zpět k periodicitě. Funkce se skládá ze tří složených funkcí spojených algebraickými operacemi. Nejprve se podíváme na každou složenou funkci.

sin(3x) má periodicitu (2π)/3, protože jde o 2π-periodický sinus, u jehož argumentu bylo změněno měřítko (viz Přehled metod - Reálné funkce - Transformace).

Druhá funkce, na kterou se podíváme, je cos(2x), která je - ze stejného důvodu - π-periodická. Můžeme dokonce přidat i tu část "+ 1", víme, že posun periodické funkce nezmění její periodu.

Třetí člen je tg³(x). Tangens je π-periodický a umocnění na třetí nemění periodu (když skládáme funkce a vnitřní je periodická, tak to ta vnější nezkazí, opět viz Přehled metod - Reálné funkce - Transformace).

Máme tedy tři funkce, jejichž periodicitu známe, a tyto jsou dány dohromady dělením a sčítáním. Pravidlo říká, že v této situaci má výsledná funkce periodu, která je nejmenším společným násobkem period jednotlivých částí. V našem případě máme periody 2π/3 a π, hledáme tedy kladné reálné číslo r takové, že r/(2π/3) je celé číslo a r/π je celé číslo. Druhá podmínka říká, že r = kπ pro nějaké přirozené číslo k, to nejmenší k takové, aby platila rovněž první podmínka, je 2.

Tvrdíme tedy, že T = 2π je periodou dané funkce.

Potvrzení:

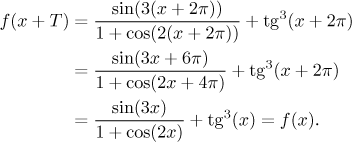
Další příklad
Zpět na Řešené příklady - Reálné funkce