Limit and comparison

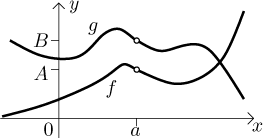
In this section we will look at the connection between comparison of functions (by inequalities) and comparison of their limits.

Theorem.
Let a be a real number, ∞, or −∞. Let f,g be functions defined on a reduced neighborhood of a, assume that f has limit A at a and g has limit B at a.
(i)     If there is a reduced neighborhood of a on which f ≤ g, then A ≤ B.
(ii)     If A < B, then there must be a reduced neighborhood of a on which f < g.

These statements look reasonable once you try to draw some pictures.

It might be even clearer if you imagine the opposite. Try to draw some picture where f ≤ g, yet the limit of g is sharply smaller than the limit of f, you should soon get the feeling that this is not possible.

Note that the theorem is true also for improper limits, it is understood that every real number is greater than negative infinity and less then infinity. As usual, the theorem is also true for one-sided limits with obvious modifications (we only use one-sided reduced neighborhoods).

It should help our understanding of a limit if we try to see why the theorem does not say more. We start with the first statement. Could we get some extra information if we use sharp inequality in the assumption? The answer is in the negative. Even if we knew that f < g everywhere, we still could not say more than what is in the theorem (for instance A < B seems tempting, but it wouldn't work), since even in such a case we can still have A = B. Indeed, consider f (x) = x² and g(x) = 0 as functions on the set U = (−∞,0) ∪ (0,∞). Then f < g on U, yet both have limit 0 at a = 0.

In the second statement it is similar. The sharp inequality there is necessary, since if we try to relax it, we run into trouble. Indeed, imagine that we know that A ≤ B. Can we say something about f and g? This time consider f (x) = x³ and g(x) = 0 as functions on the set U = (−∞,0) ∪ (0,∞). Their limits at a = 0 are both zero, so they satisfy the condition A ≤ B, but no comparison between f and g is possible on any reduced neighborhood.

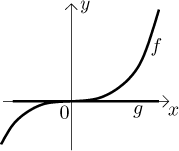
We started the theorem by assuming that we have limits. Without this assumption, no comparison of limits is possible, since from a mere comparison between f and g we cannot conclude the existence of a limit. There is an exception to this, though.

Theorem.
Let a be a real number, ∞, or −∞. Let f,g be functions defined on a reduced neighborhood of a on which f ≤ g.
If f goes to infinity at a, then also g goes to infinity at a.
If g goes to negative infinity at a, then also f goes to negative infinity at a.

This should also make sense, in the first case f pushes g up and forces it to go to infinity, the second statement is the opposite situation. Again, the theorem also works for one-sided limits.

How about proper limits? Even if we enclose a function from below and from above by convergent functions, we cannot guarantee its convergence. After all, we know that a bounded function need not converge, for example the function sin(1/x) does not have a limit at 0, although it is bounded from above by the constant function 1 (which converges to 1 at 0) and from below by the constant function −1 (which converges to −1 at 0). If we want to enforce convergence, it is not enough to enclose, we need to squeeze.

Again, the statement should seem natural once you look at a picture, g has nowhere to go but to L.

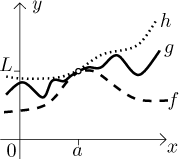
This theorem also has an analogous versions for one-sided limits. It also works for improper limits L, but for those it is unnecessarily complicated, for these we have a better comparison above.

The Squeeze theorem has some convenient corollaries:

Theorem (The Squeeze theorem - absolute value version).
Let a be a real number, ∞, or −∞. Let f,g be functions defined on a reduced neighborhood of a. Assume that there is a reduced neighborhood of a on which | f | ≤ g. If g→0 at a, then also f →0 at a.

Theorem.
Let a be a real number, ∞, or −∞. Let f,g be functions defined on a reduced neighborhood of a, assume that f is bounded on it.
(i)     If g→0 at a, then f⋅g→0 at a.
(ii)     If |g|→∞ at a, then f /g→0 at a.
(iii)     If g→∞ at a, then f + g→∞ at a.

The statement in (i) is often expressed as "zero times bounded gives zero", the statement in (ii) as "bounded divided by infinity gives zero"; one can include these among the rules of limit algebra.

Example: x⋅sin(1/x) converges to 0 at a = 0, since x tends to 0 at 0 and sin(1/x) is bounded on its domain.

For hints on the proper use of the squeeze we refer to Methods Survey, namely the box "comparison and oscillation".

L'Hospital's rule
Back to Theory - Limits