Problem: Evaluate (if it exists) the limit
![]()
Solution: This is a standard problem, we want to find a limit from the right of an expression that exists on a right reduced neighborhood of the limit point. Thus we start by substituting this point into the expression.
![]()
How did we work out those one-sided things? First, in the logarithm we substitute "1 plus", that is, numbers close to 1 and slightly greater than 1, so the outcomes are close to zero and slightly larger than zero, therefore 0+.
In the second fraction, when x is a number close to 1 satisfying
Thus we have an indeterminate difference. Combining the two parts together using algebra and cancelling somehow does not seem possible, so we try another recommended trick, using common denominator.
![]()
This looks like an indeterminate ratio, no algebraic trick seems possible, so we use the standard trick: l'Hospital's rule.
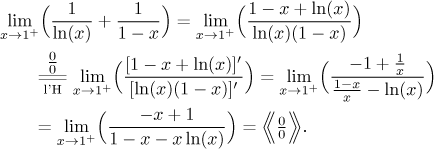
Another indeterminate ratio, it is not clear whether another l'Hospital would help, but one logarithm did disappear, so perhaps it is worth trying it again.
