Reálné funkce jsou nejdůležitějším druhem zobrazení. Poté, co je uvedeme, se podíváme na inverzní funkce a na funkce definované po částech.
Definice.
Pojem reálná funkce reálné proměnné označuje libovolné zobrazení z nějaké podmnožiny reálných čísel do reálných čísel.
Většinou se říká jen ˙reálná funkce a automaticky se tím rozumí reálná funkce reálné proměnné. Jiné typy reálných funkcí (jako například reálné funkce komplexní proměnné) jsou vždy označovány celým jménem.
Pro matematika je tato definice zcela postačující, protože si všechny vlastnosti zobrazení hbitě převede na funkce. Pro praktického uživatele to už tak vhodné není, protože reálné funkce se dají v pohodě používat i bez toho, aby člověk věděl, že nějaká zobrazení existují, asi se také pracuje lépe bez vší té přesnosti. Zkusíme zde proto ukázat, co jsou reálné funkce zač, bez pomoci zobrazení. To se nejlépe udělá příkladem a použijeme jeden inspirovaný fyzikou, protože koneckonců fyzika byla vlastně pro zavedení funkcí hlavní inspirací. Na tomto příkladě také připomeneme pojmy definičního oboru, prostoty, na a inverzní funkce, takže opravdu doporučujeme, ať se na něj podíváte. Raději jej uděláme jako samostatnou stránku, protože je dost dlouhý a taky se na něj ještě budeme odvolávat odjinud.
Teď stručně probereme základní pojmy.
Reálná funkce je předpis, který přiřazuje hodnoty k argumentům. Značení
Existuje další způsob, jak vyjádřit, že chceme do funkce dosadit nějaké konkrétní číslo. Používá mírně sníženou svislou čárku a vypadá to takto:
![]()
Toto značení se obzvláště hodí v případě, že funkce ještě není zralá na dosazení a chceme ji nejprve trochu upravit. Příklad:
![]()
Nejlepší způsob, jak si funkce vizualizovat, je pomocí grafu, kdy v
dvourozměrné rovině
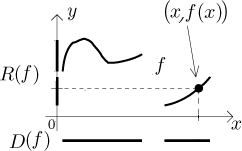
V případech, kdy je funkce zadána vzorcem, nás také může zajímat její algebraické složení, což je další způsob, jak se dívat na funkce, nezávislý na geometrickém přístupu přes grafy. Pro detaily se podívejte na poznámku o pořadí výpočtu.
Definiční obor funkce je někdy zadán při definici funkce. Mnohem
častěji jsou reálné funkce dány pouze předpisem, pak jako definiční obor
bereme množinu všech čísel x, která lze do funkce dosadit, tj. pro
která má příslušný vzorec smysl. Značí se obvykle
V typickém případě je definiční obor tvořen sjednocením intervalů.
Obor hodnot dané funkce je množina všech hodnot, kterých lze dosáhnout
dosazováním argumentů z definičního oboru do funkce. Obvykle se značí
Někdy uvažujeme danou funkci pouze na určité podmnožině definičního oboru.
Pak řekneme, že jsme udělali restrikci dané funkce na tuto podmnožinu,
nová funkce se pak nazývá restrikce. Jestliže je M podmnožina
definičního oboru
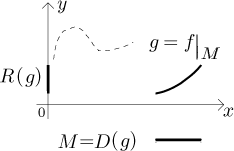
Omezená funkce pak má jiný definiční obor a může mít i jiný obor hodnot, i když to není nutné, protože někdy funkce pokryje všechny své hodnoty už na množině, na kterou jsme ji omezili, a na částech, které ignorujeme, je jen opakuje.
Vlastnosti funkcí často silně závisí na jejich definičních oborech, takže je vlastně třeba vždy myslet na funkci a její definiční obor jako na pár. Odráží se to například v následující definici.
Definice.
Řekneme, že se dvě funkce f a g rovnají, značenof = g, jestliže mají stejný definiční obor D a pro všechna x z D mámef (x) = g(x).
Podívejte se na tento příklad. Tato rovnost evidentně platí:
![]()
Teď definujeme dvě funkce.
![]()
Ačkoliv jsou tyto dva vzorce stejné algebraicky, funkce si nejsou rovny, neboli nemůžeme psát f = g, protože se liší jejich definiční obory:
![]()
Někdy nechceme uvažovat hodnoty f mimo jistou množinu M, ale pořád chceme být schopni pracovat na celém jejím definičním oboru. Pak pojem restrikce nepomůže, namísto toho můžeme hodnoty f mimo M "zabít" tímto trikem:
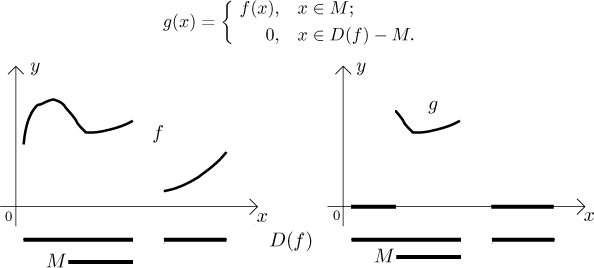
Tento přístup má několik výhod, jednou z nich je, že funkci g lze vyjádřit algebraicky, viz sekci o charakteristických funkcích v části Teorie - Elementární funkce.
Existuje alternativní metoda vizualizace funkcí. Zahrnuje méně informací o dané funkci, ale někdy je vhodná jako zdůraznění funkce coby procedury pro posílání bodů z jedné množiny do jiné. Reálná funkce vlastně posílá body z jedné kopie reálných čísel do jiné (rozdílné) kopie reálných čísel, odlišnost se zdůrazní použitím jiného písmena pro prvky dotyčných množin.
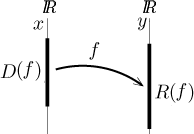
Někdy se dá dokonce přímo ukázat, jak se posílají jednotlivé body, například
funkci
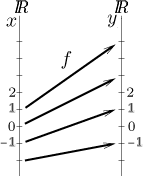
Prostota.
Řekneme, že daná funkce je prostá, jestliže se nemůže stát, že by dva argumenty byly poslány na
stejnou hodnotu. Přesně, pro prostou funkci f se nemůže stát, abychom
pro různé
V praxi je snažší pracovat s jinou podmínkou, formálně s obměnou té předchozí: Jestliže po dosazení dvou bodů do funkce dostaneme stejnou hodnotu, pak to musel být stejný bod.
Definice.
Řekneme, že funkce f je prostá (nebo injektivní nebo injekce), jestliže pro všechnax1,x2 z jejího definičního oboru platí následující implikace: Jestližef (x1) = f (x2), pakx1 = x2.
Pokud nám také byla s funkcí f zadána cílová množina B, můžeme
se zeptat, jestli je f na (nebo surjektivní nebo
surjekce), neboli jestli je cílová množina rovna oboru hodnot,
Funkce je bijektivní (bijekce), jestliže je prostá a na. U reálných funkcí se staráme jen o prostotu.
Inverzní funkce k funkci f (nebo krátce její inverze) je
funkce g splňující následující podmínky:
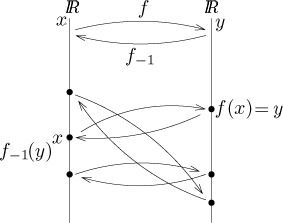
Pokud takováto inverzní funkce existuje, značíme ji
Známá věta říká, že inverze existuje právě tehdy, když je daná funkce bijekce. Pro reálné funkce máme nicméně speciální verzi.
Věta.
Nechť f je reálná funkce s definičním oboremD( f ) a oborem hodnotR( f ). Tato funkce má svou inverzi právě tehdy, jestliže je prostá. Tato inverze je pak jednoznačně určena a splňuje
D( f−1) = R( f ), R( f−1) = D( f ).
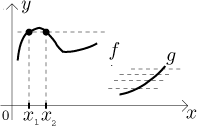
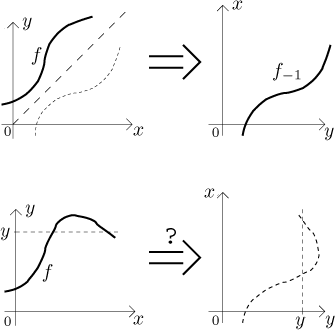
Graf inverzní funkce se dá získat tak, že se graf f překlopí okolo hlavní diagonály. Toto mimochodem ukazuje, proč je prostota důležitá pro existenci inverze. V následujícím obrázku nejprve máme ukázku funkce, která má inverzi. Druhý obrázek ukazuje funkci, která není prostá (k vyznačené hodnotě y se dostaneme ze dvou míst). Vidíte, že když zkusíme překlopit její graf, dostaneme něco, co rozhodně není grafem funkce, protože funkce nemůžem mít pro jeden argument dvě hodnoty.
K inverzi se vrátíme v následující sekci Operace s reálnými funkcemi, jmenovitě když se tam probírá skládání.
Příklad. Uvažujme funkci
Nejprve se musíme podívat na definiční obor. Jaká čísla x lze dosadit
do daného vzorce? Víme, že umocnit na druhou lze libovolné číslo, takže
odpověď zní: Všechna reálná čísla. Proto
Obor hodnot je obvykle mnohem méně důležitý, je také často docela obtížné jej
zjistit, takže většinou se tím nenamáháme. Zde je to nicméně docela snadné,
tak to zkusíme. Jaké hodnoty lze dostat pomocí vzorce definujícího
f ?
Ze zkušenosti víme, že druhé mocniny jsou vždy kladné či přinejmenším nula,
takže vzorec
Jak je to s prostotou a inverzí? Víme, že tyto dvě otázky jsou ekvivalentní.
Abychom odpověděli na první, zkusíme dokázat implikaci z definice, tedy předpokládáme,
že
(1 − x1)2 =
(1 − x2)2.
Víme, že tato rovnice má dvě možná řešení. Jedno je
Potvrdili jsme, že dvěma rozdílným argumentům, 0 a 2, je přiřazena tatáž hodnota, jmenovitě 3. Funkce f proto není prostá a ani nemá inverzi.
Můžeme také zkusit najít inverzní funkci a uvidíme, jestli se to povede. Aby
inverze existovala, měli bychom být schopni obrátit přiřazení
Víme, že tato rovnice má dvě různá řešení, jmenovitě x se může rovnat
1 mínus odmocnina z
Správné kreslení grafu se probírá až později v sekci Průběh funkce v části Derivace - Teorie, takže abychom teď získali alespoň nějakou představu o grafu naší f, zkusíme na něm najít nějaké body, jinými slovy, spočítáme hodnoty f v mnoha bodech x. Samozřejmě, čím více tím lépe, ale pro jednoduchost jich zde zkusíme jen pár:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Znázorníme je ve grafu:
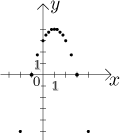
Body zhruba naznačují tvar. Ve skutečnosti je přesným tvarem dolů otočená parabola:
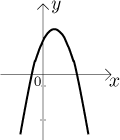
Hned vidíme, že tato funkce není rozhodně prostá, protože s výjimkou
vrcholu
Z obrázku také vidíme, že když tuto funkci omezíme jen na jednu větev
paraboly (či dokonce jen její kousek), stane se prostou. Uvažujme například
funkci g získanou restrikcí f na otevřený interval
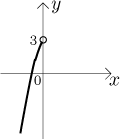
Tato funkce je teď prostá a má inverzi, což potvrdíme tak, že ji úspěšně
najdeme. Potřebujeme vyřešit rovnici
![]()
Inverzní funkci jsme tedy našli, tím také dokázali její existenci a to, že
funkce g je prostá. Inverzní funkce má definiční obor
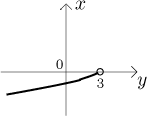
Všimněte si, že jsme zcela přirozeně pro inverzní funkci dostali y
jako proměnnou. Protože ve většině případů se dává přednost proměnné
x, lidé často při hledání inverzní funkce prohodí proměnné a nakonec by psali
Všimněte si, že pokud si zvolíme jinou restrikci na levé polovině paraboly,
například na množinu
Poznámka:
Když jsme se bavili o inverzi
Více opatrnosti je třeba v případě, kdy je ve hře více písmen, třeba když
definice funkce závisí na nějakém parametru p. Například vzorec
Některé funkce nejsou definovány jen jedním vzorcem, ale několika, některé argumenty se dosazují do jednoho vzorce, jiné do jiného vzorce. Říkáme, že taková funkce je definována "po částech", a typický příklad je například tento:
![]()
Jak to funguje? Argumenty, pro které umíme počítat f, se dají brát z
uzavřeného intervalu
Když chceme dosadit nějaké x z definičního oboru, nejprve se podíváme,
do které alternativy spadá, podle toho pak použijeme příslušný vzorec.
Například
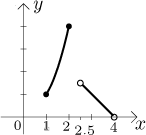
A přesně tak se také zkoumají funkce definované po částech. Každý případ se zkoumá zvlášť, grafy a odpovědi se pak dají dohromady. Mohou se také objevit zajímavější podmínky, například funkce
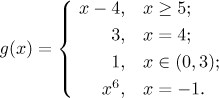
Ta má definiční obor
a graf
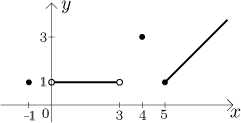
Některé hodnoty:
Tato idea - dávat funkci dohromady po kouskách - se používá nejen u funkcí
definovaných po částech, ale také u funkcí definovaných jedním vzorcem, které
ale mají definiční obor sestaven z více částí. Například funkce
Někdy je funkce dána jen jedním vzorcem, ale definice po částech je v něm skryta, což je především příklad absolutní hodnoty.
Pro více informací o funkcích definovaných po částech viz sekce Funkce definované po částech v časti Derivace - Teorie - Průběh funkce.