Konvexita a inflexní body: Přehled metod

Nechť f je "rozumná" funkce, což zde znamená, že se její definiční obor dá rozdělit na nejvýše spočetně mnoho intervalů, na každém z nichž je funkce dvakrát diferencovatelná. Chceme určit intervaly konvexity a inflexní body.

Algoritmus:
Krok 1. Určíme intervaly definičního oboru f.
Krok 2. Najdeme druhou derivaci f ′′. Najdeme body, kde f ′′(x) = 0 nebo f ′′ neexistuje. Tyto body rozdělí intervaly z Kroku 1 na intervaly konvexity.
Krok 3. Pro každý z intervalů z Kroku 2 určíme znaménko druhé derivace. Obecná metoda: Dosadíme bod z vnitřku takového intervalu do f ′′ a zjistíme znaménko.
Speciální metoda pro druhé derivace, které jsou součiny/podíly faktorů: Určíme znaménko každého faktoru zvlášť a pak násobíme znaménka pomocí standardní znaménkové algebry. To se nejlépe dělá tabulkou (viz Příklad níže).
Krok 4. Určíme konvexitu ze znamének f ′′. Funkce f je konvexní na intervalech, kde je f ′′ kladná. Je konkávní na intervalech, kde je f ′′ záporná.
Když píšeme v odpovědi intervaly, uzavřeme koncové body, kde je f spojitá z příslušné strany.
Krok 5. Určíme inflexní body jako body definičního oboru, kde se mění konvexita.

Pro pozadí tohoto algoritmu viz Konvexita a inflexní body v části Teorie - Průběh funkce.

Příklad: Určete konvexitu a inflexní body funkce

Řešení: D( f ) = (−∞,−1) ∪ (−1,∞). Začneme se dvěma intervaly.

Dělící body: f ′′(x) = 0 dává x = 0, kvadratický polynom kořeny nemá; v definičním oboru nejsou body, kde by druhá derivace neexistovala, takže další dělící body už nebudou. Dostali jsme tři intervaly. Dáme je do tabulky, použijeme uzavřené konce tam, kde je f spojitá z příslušné strany. Do řádků dáme jednotlivé faktory druhé derivace a určíme jejich znaménka na všech intervalech, pak uděláme závěr.

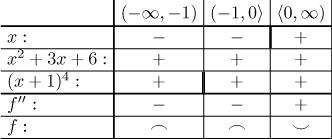
Závěr: f je konkávní na (−∞,−1) a na (−1,0⟩, je konvexní na ⟨0,∞). Má inflexní bod f (0) = 2.

Mimochodem, pokud chcete vidět, jak tato funkce vypadá, podívejte se na Příklad v sekci Přehled metod - Průběh funkce - Přehled).

Poznámka: Metoda tabulkou má jednu výhodu, není nutné dosazovat body z intervalů do derivace (nebo jejích faktorů). Pokud je faktor lineární, pak mění znaménko jen jednou, jmenovitě v bodě, kde je nula. Stačí si tedy v tabulce poznamenat, kde je tento dělící bod, a pak dát jedny znaménka doprava a opačná doleva. Má to jít − + nebo + −? To se snadno pozná, stačí dosadit jiný bod než ten dělící, dokonce je možné se zeptat, co se stane, když x jde do nekonečna, zda se faktor stane kladným nebo záporným. Pro další pohled na tuto věc viz Nerovnice se znaménky v sekci Řešíme rovnice a nerovnice v části Extra.

Pro další příklady viz Konvexita a inflexní body v části Teorie - Průběh funkce a příslušné příklady v části Řešené příklady.

Asymptoty
Zpět na Přehled metod - Průběh funkce