Předpokládejme, že funkce f je rozumná, což zde znamená, že se její definiční obor skládá z nejvýše spočetně intervalů takových, že je na každém z nich dvakrát diferencovatelná. Abychom načrtli graf takovéto funkce, používáme tento postup.
Algoritmus kreslení průběhu funkce:
Krok 1. Určíme definiční obor f, průsečíky s osami (pokud je to
možné), symetrii a periodicitu, spojitost (někdy s pomocí limit z Kroku 2).
Pro detaily o těchto tématech viz
Funkce - Přehled metod
- Reálné funkce.
Krok 2. Najdeme příslušné jednostranné limity ve všech krajních bodech
intervalů z definičního oboru f, případně také intervalů z definice
f. Pro informace o limitě viz
Funkce - Přehled metod
- Limita. Kde je to možné, interpretujeme tyto výsledky jako asymptoty, v
případě nutnosti včetně algoritmu pro šikmé asymptoty, viz
Přehled metod - Průběh funkce -
Asymptoty.
Krok 3. Najdeme derivaci f ′. Pomocí ní určíme intervaly
monotonie a lokální extrémy, pro více informací viz
Přehled metod - Průběh funkce -
Monotonie a lokální extrémy.
Krok 4. Najdeme druhou derivaci f ′′. Pomocí ní určíme
intervaly konvexity a inflexní body, pro více informací viz
Přehled metod - Průběh funkce -
Konvexita a inflexní body.
Krok 5. Nakreslíme graf. Jsou dvě strategie:
1) Při každém kroku tohoto postupu rovnou zanášíme získaná data do obrázku, v
každém kroku obrázek zpřesňujeme.
2) Nejprve uděláme všechny výpočty, pak dáme do obrázku všechna body, pak
zkombinujeme informaci o monotonii a konvexitě a vytvoříme konečný tvar. Pro
detaily viz
Složky správného kreslení grafů v
části Teorie - Průběh funkce.
Příklad: Načrtněte půběh funkce
![]()
Řešení:
Průsečíky:
Limity v koncových bodech:
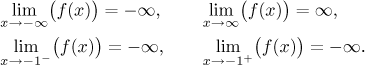
Vidíme, že v
Najdeme derivaci a pomocí ní určíme, že f je rostoucí na
Najdeme druhou derivaci a pomocí ní určíme, že f je konkávní na
Výpočty jsou hotovy, je čas na obrázek. Nakreslíme souřadnicové osy a zaznačíme všechny body a limity v koncových bodech, abychom graf ukotvili.
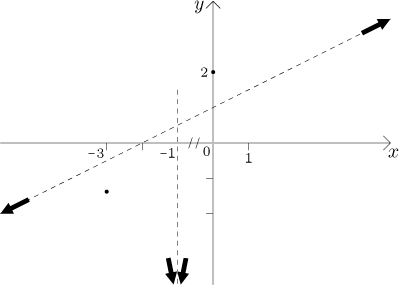
Teď spojíme tabulky monotonie a konvexity, abychom měli lepší představu o tvaru grafu.
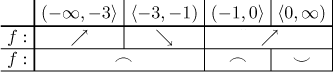
Nakonec tento tvar "pověsíme" na kotevní body a dostaneme graf, použijeme ještě informaci o vodorovné tečně v 0.
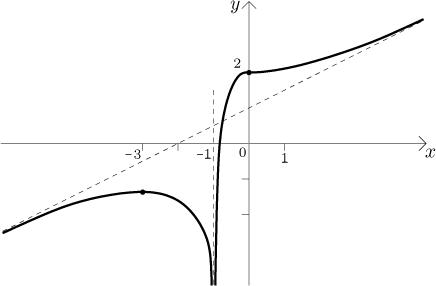
Poznámky:
Pokud by funkce, kterou kreslíme, měla vlastní limitu v některém vlastním
koncové bodě (viz Krok 2), pak potřebujeme vědět, kterým směrem máme začít
kreslit graf z toho bodu. To zjistíme tak, že spočítáme příslušnou
jednostrannou derivaci v dotyčném bodě, nejspíše pomocí limity, a v tomto
případě nemusíme vyžadovat spojitost, viz
tato poznámka.
2. Jestliže je f funkce daná rozpisem, pak je nejlepší strategie dělat všechny kroky zároveň pro všechny výrazy definující tuto funkci a rovnou spojovat informace. Pro podrobnosti viz sekce Funkce dané rozpisem v části Teorie - Průběh funkce, viz také tento příklad v části Řešené příklady - Průběh funkce.
3. Jestliže f obsahuje absolutní hodnotu (nebo více absolutních hodnot), pak je třeba začít tím, že se jich zbavíme a zapíšeme tuto funkci jako funkci danou rozpisem. Viz příslušný příklad v části Řešené příklady - Průběh funkce.
Pro další příklady viz Složky správného kreslení grafů v části Teorie - Průběh funkce a příslušné příklady v části Řešené příklady.
Monotonie a lokální extrémy
Zpět na Přehled metod - Průběh
funkce