Příklad: Určete maximální intervaly monotonie a lokální extrémy funkce

Řešení: Jako obvykle začneme definičním oborem. V daném výrazu není žádný problém, takže definiční obor je celá reálná osa. Začínáme tedy s jedním intervalem, teď zjistíme, jestli jej není třeba rozdělit, abychom získali intervaly monotonie. Potencionální dělící body získáme nalezením kritických bodů. Nejprve najdeme derivaci; kvůli absolutní hodnotě ale nemůžeme použít pravidla. Standardní trik je zbavit se absolutní hodnoty rozdělením funkce.

Teď už můžeme každý z výrazů derivovat pomocí obvyklých pravidel, ale musíme si pamatovat, že takové derivování funguje jen na otevřených množinách.

Nevíme, zda máme derivaci v bodě 3. Mohli bychom to zjistit pomocí jednostranných derivací, ale není to vlastně nutné, protože teď hledáme kritické body kvůli monotonii. V x = 3 možná derivace neexistuje, tak ho přidáme na náš seznam dělících bodů. Další kritické body se najdou tím, že se zeptáme, kde je derivace rovna nule.

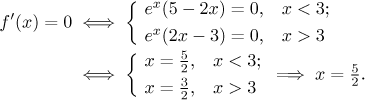
Ignorovali jsme x = 3/2; je to sice řešení rovnice e^x(2x − 3) = 0, ale tento výraz nemá nic společného s f ′ pro x < 3.

Máme dva dělící body, což znamená tři intervaly a monotonii na nich určíme pomocí tabulky. Uzavřeme koncové body intervalů tam, kde je funkce spojitá. Jako obvykle u funkcí definovaných rozpisem musíme dát pozor na to, abychom každý vzorec použili jen v oblastech, kde je platný.

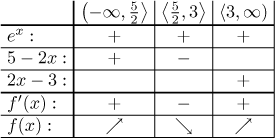
Vidíme, že se v bodě 3 opravdu mění monotonie, takže jsme jej oprávněně přidali na seznam. Závěr je, že daná funkce je rostoucí na (−∞,5/2⟩ a na ⟨3,∞) a je klesající na ⟨5/2,3⟩. Zbývá určit lokální extrémy.

Funkce f má lokální maximum f (5/2) = 2e^5/2 a lokální minimum f (3) = e³.

Další příklad
Zpět na Řešené příklady - Průběh funkce