Aproximace funkcí tečnami

Uvažujme následující situaci. Máme funkci f a chceme znát její hodnotu v určitém bodě x. Jenže dosazování x do výrazu dávajícího f není zrovna příjemné, na druhou stranu je tady bod a blízko x, který by nám dosazovat do f vůbec nevadilo. Je nějaký způsob, jak pomocí něj alespoň aproximovat f (x)?

V případech, kdy je dosazování a do f snadné, obvykle také nemáme problém s dosazováním a do f ′. To znamená, že můžeme najít tečnu T ke grafu f v a. Jestliže je x opravdu blízko k a, pak je f (x) asi skoro totéž jako T(x), takže tím druhým můžeme aproximovat to první.

Řešení: Máme sice algoritmus pro počítání druhé odmocniny tužkou na papíře, ale skoro nikdo si jej nepamatuje. Zkusíme tedy něco jiného. Označíme druhou odmocninu x jako f (x) a použijeme k aproximaci této funkce tečnu. Chceme f (5), potřebujeme tedy bod a, který je blízko k x = 5 a zároveň je snadné z něj udělat odmocninu. Je jasné, že zvolíme a = 4. Spočítáme tečnu k f v a:

Můžeme tedy aproximovat odmocninu z 5 neboli f (5) výrazem T(5) = 9/4 = 2.25.

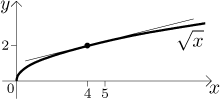
Takové aproximace tečnami jsou docela užitečné. Lidé, kteří často pracují s druhými odmocninami čísel blízkých k 1, mohou ocenit aproximaci

která funguje dost dobře pro |x| < 0.2. Vlastně jste aproximaci tečnami viděli ve fyzice na základce či na střední škole, ačkoliv jste o tom asi nevěděli.

Příklad: Uvažujme těleso o hmotnosti m, zajímá nás jeho potenciální energie vzhledem ke gravitaci Země. Budeme předpokládat, že je Země kulatá (s poloměrem R) a homogenní, což není tak úplně pravda, ale je to skoro tak. Pak se síla F, zrychlení a a potenciální energie U_g takového tělesa, které je ve vzdálenosti r od středu Země, spočítá jako

Tohle se ale studenti na střední škole neučí. Zkusíme si situaci trochu zjednodušit. Nemáme v úmyslu se zavrtávat do Země nebo lítat moc vysoko, takže si jako výchozí bod vezmeme poloměr Země R. Zrychlení u tohoto poloměru se tradičně značí g, takže to můžeme dát do toho vzorečku pro zrychlení, vyjádřit M a dosadit do U_g:

Pak má také smysl měřit potenciální energii vzhledem k povrchu Země. Použijeme h pro výšku onoho tělesa nad povrchem, tedy r = R+h, a jsme připraveni uvést relativní potenciální energii:

U(h) = U_g(R+h) - U_g(R).

Dostali jsme rozdíl dvou zlomků, kde je proměnná h ve jmenovateli, což není moc příjemné. Pokud očekáváme, že nebudeme vzdálenost měnit nějak zásadně, má smysl zkusit aproximovat U_g tečnou vzatou v r = R, tj. pro h = 0.

Pokud dosadíme toto namísto U_g(R+h), dostaneme vzorec, který známe ze střední školy:

U(h) = gmh.

Popravdě řečeno, docela dost "zákonů", které jste se učili ve středoškolské fyzice, jsou jen aproximace obecnějších a komplikovanějších zákonů tečnami. Tyto aproximace obvykle velmi dobře fungují v rozumných mezích, například ten vzorec pro potenciální energii funguje velmi dobře v rozmezí výšek, kde se lidé nejčastěji pohybují.

Při aproximaci tečnami samozřejmě děláme určitou chybu a nevíme, jak velkou, například nevíme, jak dobrý je ten odhad, který jsme dostali pro odmocninu z 5. Pro nějaké odpovědi (a lepší aprocimaci) navštívte další sekci. Pro příklady se podívejte do Řešených příkladů - Aplikace, zajímavé použití lze najít v tomto příkladě v části Řady - Řešené příklady - Testování konvergence.

Taylorův polynom
Zpět na Teorie - Aplikace