Příklad: Určete, zda následující řady konvergují.

Řešení: Začneme s první řadou. Její tvar nás nabádá, abychom použili odmocninové kritérium.

Protože ϱ < 1, první daná řada konverguje. Všimněte si, že už nepomůže žádný jiný test s výjimkou podílového kritéria, ale limita v něm je dost drsná na výpočet.

Teď přejdeme k druhé dané řadě. Bude zase odmocninové kritérium tak pěkné? Tentokráte dostaneme neurčitou mocninu a musíme použít příslušný trik, viz Posloupnosti - Přehled metod - Limita.

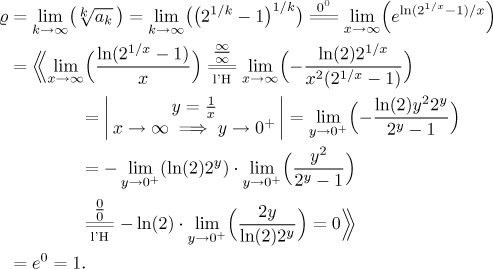
Takže v tomto případě odmocninové kritérium nepomůže, podílové kritérium by bylo evidentně také neurčité a musíme se tedy poohlédnout jinde. Funkce f (x) = 2^1/x − 1 je sice klesající a kladná, ale neuměli bychom ji integrovat, a tak je integrální kritérium mimo hru.

Jak je to se srovnáním? Jedno jasné se nabízí.

ale protože velká řada napravo diverguje (její členy nejdou k 0), je to na nic. Co se dá ještě dělat? Probírat se podílem následujících členů vypadá dost špatně, takže asi není dobrým nápadem zkoušet různá ještě komplikovanější vylepšení podílového kritéria (jako Raabeho kritérium a tak). Můžeme zkusit jít na to jinak: Co víme o a_k pro velká k? Pak je 1/k velmi malé a kladné, můžeme zkusit aproximovat 2^y okolo počátku pomocí jeho tečny, abychom dostali něco pěknějšího. Máme

takže můžeme odhadnout, že pro velké hodnoty k máme

Pokud chceme použít limitní srovnávací kritérium, pak takové tvrzení musíme dokázat.

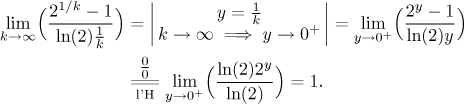
Takže jsme ospravedlnili srovnání

Protože testovací řada napravo diverguje (je to ta slavná harmonická řada, případně se podívejte na p-test), vyplývá z toho, že také daná řada diverguje.

Další příklad
Zpět na Řešené příklady - Testování konvergence