Globální extrémy, optimalizace: Přehled metod

Máme zde tři témata: globální extrémy, globální extrémy s podmínkami a optimalizaci.

Problém: Najděte globální extrémy funkce f na množině M.

Případ 1: Funkce je spojitá na M, což je omezená uzavřená množina sestávající se z konečného počtu uzavřených intervalů. Pak vždy existuje maximum a minimum.

Algoritmus:
Krok 1. Shromáždíme kandidáty. Jde o tyto: a) všechny koncové body z intervalů M; b) všechny body z M, kde je derivace f ′ nulová nebo neexistuje (nebo máme podezření, že neexistuje).
Krok 2. Dosadíme všechny kandidáty do f a porovnáme výsledné hodnoty. Bod, který dává největší z těchto hodnot, dává max_M( f ). Bod, který dává nejmenší z těchto hodnot, dává min_M( f ). Poznamenejme, že maximum a minimum nemusí být jednoznačné.

Případ 2: Funkce má konečný počet nespojitostí na M, což je konečné sjednocení intervalů.

Algoritmus:
Krok 1. Shromáždíme kandidáty. Jde o tyto: a) všechny koncové body intervalů z M (včetně nekonečna/mínus nekonečna, pokud je to koncový bod); b) všechny body z M, kde je derivace f ′ nulová nebo neexistuje (nebo máme podezření, že neexistuje). Všimněte si, že toto zahrnuje i všechny body (podezřívané) nespojitosti.
Krok 2. Dosadíme do f ty kandidáty, kde je f definovaná; pro ty kandidáty, kde f definovaná není (otevřené koncové body intervalů, což mohou být i nevlastní body) nebo kde f nemusí být spojitá, také vyhodnotíme všechny možné jednostranné limity. Všechny obdržené hodnoty (dosazením i limitou) porovnáme.
Krok 3. Jestliže je největší hodnota dosažená (také) dosazením kandidáta, pak dosazený bod dává max_M( f ). Jestliže je největší hodnota (může být i nevlastní) dosažená pouze limitou, pak f nemá maximum na M.
Jestliže je nejmenší hodnota dosažená (také) dosazením kandidáta, pak dosazený bod dává min_M( f ). Jestliže je nejmenší hodnota (může být i nevlastní) dosažená pouze limitou, pak f nemá minimum na M.

Pro detaily viz Globální extrémy v části Teorie - Aplikace.

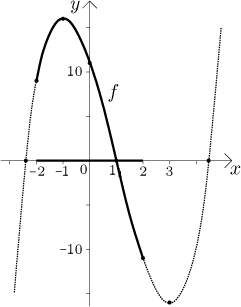
Příklad: Najděte maximum a minimum funkce f (x) = x³ − 3x² − 9x + 11 na množině M = ⟨−2,2⟩.

Řešení: Protože je f spojitá na M, což je omezený uzavřený interval, tak existují jak maximum tak minimum a můžeme použít první algoritmus.

Derivace je f ′(x) = 3x² − 6x − 9 = 3(x² − 2x − 3). Existuje všude, její nulové body jsou −1 a 3. Ale 3 neleží v M, takže máme jednoho kandidáta, jmenovitě x = −1. Jsou dva další kandidáti, koncové body x = −2 a x = −2. Dosadíme do f:

f (−2) = 9,   f (−1) = 16,   f (2) = −11.

Porovnáme tyto hodnoty a odvodíme závěr:

max_⟨−2,2⟩( f ) = f (−1) = 16,   min_⟨−2,2⟩( f ) = f (2) = −11.

Mimochodem, graf f ukáže, co se vlastně během našeho výpočtu děje.

Problém: Potřebujeme najít globální extrémy funkce více proměnných, ale proměnné jsou svázány podmínkami, kterých je o jednu méně než proměnných.

Řešení: Použijeme podmínky k tomu, abychom se zbavili všech proměnných s výjimkou jedné, pak jsme v situaci, kdy můžeme použít již popsané algoritmy.

Pro příklady na globální extrémy a globální extrémy s podmínkami viz Globální extrémy v části Teorie - Aplikace a Řešené příklady - Aplikace.

Slovní úlohy (optimalizace)

Typická slovní úloha na optimalizaci popisuje nějakou situaci a pak se zeptá na řešení, které je optimální vzhledem k nějakému hodnocení (cena atd.).

Algoritmus:
Krok 1. Pečlivě přečteme příklad a identifikujeme všechny důležité kvantity. S jejich pomocí vyjádříme údaje poskytnuté v zadání.
Krok 2. Určíme kvantitu, která se používá k vyhodnocování různých řešení. Tato kvantita se má maximalizovat/minimalizovat. Pokud má jen jednu proměnnou, můžeme použít výše popsaný algoritmus. Jinak musíme najít nějaké vztahy mezi proměnnými, abychom s jejich pomocí snížili počet proměnných na jednu. Pak už použijeme ten algoritmus.

Příklad: Máme dva přístupové body, každý na jiném břehu přímé řeky široké 16 m, jeden je 50 m po proudu od druhého. Potřebujeme je spojit kabelem, a to co nejlevněji, ale kabel po souši stojí jen 3 na metr, zatímco kabel ve vodě stojí 5 na metr. Přes vodu musíme, nejkratší cesta vede přímo mezi body, ale když vezmeme v úvahu cenu, pak je možná lepší vést kabel přímo k protějšímu břehu (nejkratší cestou, ať redukujeme co nejvíce drahou cást) a dodělat zbytek levnějším způsobem. Nebo možná nějaký kompromis by fungoval ještě lépe. Jaký způsob je nejlevnější?

Řešení: Je jasné, že nemá smysl zkoušet jiné trajektorie než přímé cesty přes vodu a pak po břehu. Co není známo? Místo na protějším břehu, kam máme zamířit. Na označení potřebujeme proměnnou, také potřebujeme rozhodnout, kde je nula, asi nejpřirozenější je dát nulu přesně naproti.

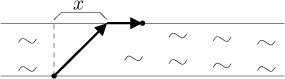
Hodnota, kterou máme minimalizovat, je cena C. Máme jednu proměnnou x a optimalizovanou funkci C, která na x závisí, potřebujeme vědět jak. Vzdálenost po souši je evidentně 50 − x, pro vzdálenost po vodě použijeme Pythagorovo pravidlo. Dostaneme

Chceme najít minimum této funkce na intervalu ⟨0,50⟩, protože nemá smysl jít směrem od cíle nebo za něj. Použijeme výše popsaný algoritmus, nejprve najdeme derivaci C a položíme ji rovnu nule.

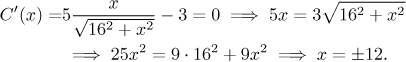
Záporné řešení je na nic, máme tedy prvního kandidáta, x = 12, a pak koncové body x = 0 a x = 50. Dosadíme do C:

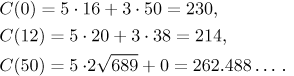
Vidíme, že nejrychlejší cesta k pití je překonat řeku směrem k bodu na protější straně, který je 12 metrů od kolmice.

Pro další příklady viz Globální extrémy v části Teorie - Aplikace a v části Řešené příklady - Aplikace.

Taylorův polynom a aproximace
Zpět na Přehled metod - Aplikace