V sekci Základní vlastnosti v části Funkce - Teorie - Reálné funkce jsme uvedli pojem globálního extrému a jeho nabytí. Je-li dána funkce definovaná na množině M, pak obecně není existence maxima a minima zaručena. Pokud je ale funkce na M spojitá a množina je omezená a uzavřená, pak maximum a minimum máme (viz Věta o extrémní hodnotě v sekci Spojitost v části Funkce - Teorie - Reálné funkce). To se samozřejmě také týká funkcí spojitých na omezených uzavřených intervalech. Na takových intervalech dokonce máme charakterizaci možných globálních extrémů (na to ale spojitost nepotřebujeme).
Věta.
Nechť je f definovaná na omezeném uzavřeném intervalu I. Jestliže f nabývá svého globálního extrému v bodě c, pak buď má f lokální extrém v c nebo je c koncový bod I.
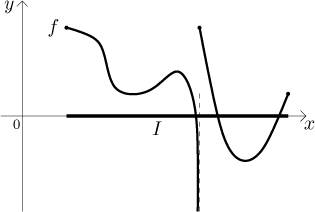
Obrázek ukazuje funkci, která má dokonce dvě globální maxima, jedno v koncovém bodě a jedno, které je i lokální maximum. Ukázali jsme zde, že malá nespojitost nemusí maximum pokazit. Vidíme ale také, že tato nespojitost zabránila existenci globálního minima.

Tato věta je velmi užitečná, protože zužuje množinu možných kandidátů. Jak například najdeme globální maximum?
1. Začneme s případem spojité funkce na omezeném uzavřeném intervalu, protože pak tam určitě takové maximum je. První krok je sebrat všechny možné kandidáty, takže podle věty tuto množinu dostaneme tak, že vezmeme koncové body intervalu a přidáme všechny lokální extrémy ležící v I, pro jejich nalezení můžeme použít derivaci, pokud je tedy f diferencovatelná (viz. Monotonie a lokální extrémy v části Teorie - Průběh funkce).
Druhý krok je vybrat mezi těmito body globální maximum. Jak jej poznáme? Globální maximum je největší hodnota, které funkce nabývá. Takže prostě dosadíme všechny kadidáty do f a porovnáme takto obdržené hodnoty, ta největší je globální maximum.
Je jasné, že když zvolíme nejmenší hodnotu, dostaneme globální minimum.
Pokud funkce není spojitá, pak tento algoritmus selže. Například v tom obrázku výše můžeme porovnávat hodnoty v koncových bodech a ta dvě lokální minima, která tam vidíme, ale ta nejmenší hodnota z nich nebude globální minimum, protože funkce jde do mínus nekonečna v bodě nespojitosti (zleva). Správná odpověď tedy je, že globální minimum neexistuje, ale z výše popsaného algoritmu to nepoznáme.
Popsaný algoritmus je docela užitečný, ale jeho podmínky jsou příliš omezující. Dají se nějak uvolnit? Jedna možnost je povolit také otevřené koncové body v intervalu. Takové koncové body se pak nedají dosadit, ale je možné tam najít příslušnou jednostrannou limitu a použít ji místo hodnoty. Pak ale bude třeba modifikovat algoritmus. Například na následujícím obrázku máme vlevo globální maximum, ale vpravo nic takového není.

Jaký je mezi těmito příklady rozdíl? Kdyby byl interval na druhém obrázku uzavřený na svém pravém konci, pak bychom tam měli globální maximum. My jsme ale ten bod odebrali a pokazili to. To naznačuje, jak by měl být algoritmus modifikován.
2. Teď budeme předpokládat, že f je spojitá na intervalu I, který nemusí být uzavřený ani omezený. První krok je stejný, shromáždíme koncové body a lokální extrémy z I. V druhém kroku je změna. Dosadíme všechny kandidáty, kteří jsou v I, a pokud některý z koncových bodů není zahrnut v intervalu, tak místo dosazení použijeme limitu. Pak porovnáme hodnoty a určíme největší/nejmenší. Pokud je taková hodnota nabyta v bodě, který náleží do I (jinými slovy, dostali jsme ji dosazením), pak dostaneme příslušný globální extrém. Pokud je ale největší/nejmenší hodnota nabyta pouze limitou, pak nemáme globální maximum/minimum.
Vidíme, že "chybějící body" komplikují situaci, jen když ovlivňují největší/nejmenší hodnotu, což poznáme porovnáním limit a hodnot získaných dosazením. Tato obecná myšlenka se dá také použít pro práci s funkcemi s konečně mnoha nespojitostmi. Přidáme body nespojitosti na seznam kandidátů,pro každý z nich se podíváme na hodnotu přímo v bodě a také na všechny možné jednostranné limity. Pak porovnáme hodnoty, a pokud je největší hodnota dosažená pouze limitou (limitami), pak není globální maximum. Podobně to funguje pro globální minimum. Dostaneme tak algoritmus, který funguje pro všechny intervaly a funkce, které mohou být občas nespojité. Jako příklad se podíváme znovu na ten úplně první obrázek, tentokráte ale přidáme pár hodnot a uděláme interval napravo neomezený.
Příklad: Použijte popsaný algoritmus pro určení globálních extrémů
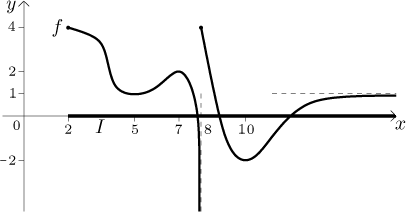
Řešení: Seznam kandidátů: koncové body 2 a nekonečno (zde použijeme limitu), lokální minima v 5 a 10, lokální maximum v 7 a bod nespojitosti v 8 (tam dosadíme a podíváme se na jednostranné limity). Hodnoty k porovnání:

Podíváme se , která hodnota je největší, a zjistíme, že hodnota 4 je nabyta jednou limitou a (což je důležité) také dvěma body. Máme tedy globální maximum, jmenovitě
maxI( f ) = f (2) = f (8) = 4.
Nejmenší "hodnota" je
Zde máme následující problém. Hledáme globální extrémy funkce f, ale tentokráte má f více než jednu proměnnou. Je to ale ve skutečnosti jednorozměrný problém, protože v řešení, které hledáme, musí proměnné splňovat určité podmínky, přičemž počet podmínek je o jednu menší, než je počet proměnných.
Můžeme tedy tyto podmínky použít k eliminaci všech proměnných kromě jedné z výrazu pro f a dostaneme standardní problém na globální extrémy, který můžeme řešit již popsaným algoritmem.
Poznamenejme, že typ problému, na který se zde díváme, je jen speciálním případem mnohem obecnější úlohy. Počet podmínek nemusí být vždy přesně o jednu menší než počet proměnných, pak je ale třeba použít pokročilejší metody, například metodu Lagrangeových multiplikátorů. To je ale částí teorie více proměnných. Zde se podíváme na příklady, které lze (v zásadě pomocí selského rozumu) převést na hledání globálních extrémů obyčejné funkce.
Příklad: Zjistěte, jako rozměry obdélníka dají maximální obsah, je-li dáno, že jeho obvod musí být 40.
Řešení: Nejprve určíme data. Obdélník je dán dvěma sousedními
stranami, takže máme proměnné x a y. Kvantita, kterou máme
maximalizovat, je obsah
Použijeme tuto podmínku k tomu, abychom se zbavili jedné proměnné v
A, řekněme
Shromáždíme všechny kandidáty. Abychom našli podezřelé body pro lokální
extrémy, podíváme se na derivaci:
![]()
Maximální obsah dostaneme pro
Problémům tohoto typu se říká příklady na optimalizaci. V dané situaci máme mnoho možných řešení, ale my hledáme jedno, které je optimální, tj. nejlepší z určitého úhlu pohledu. Tento úhel pohledu je popsán funkcí, někdy zvanou nákladová funkce, a tu my chceme maximalizovat či minimalizovat podle situace. Podmínky pak popisují situaci, za které optimalizujeme.
Tomuto typu otázek se také říká slovní úlohy a mezi studenty nejsou zrovna dvakrát populární. Upřímně řečeno, není mi jasné proč, protože v principu je to docela snadné. Myslím, že hlavní problém je s transformací slov daného problému ve vzorce. První krok (kdy uvedeme vhodné proměnné a funkce, vyjádříme jimi data z "povídání" a najdeme rovnice popisující situaci) je zásadní a zároveň nesnadný pro nezkušeného studenta. Věc ještě zhoršuje to, že pro tento krok není nějaký spolehlivý algoritmus, každý příklad je jiný. Když ale získáte nějakou zkušenost, mělo by to začít vypadat snadněji. Pro další (možná zajímavější?) příklady se podívejte do Řešených příkladů - Aplikace. Pro stručný přehled a další příklad viz Globální extrémy v části Přehled metod - Aplikace.