Příklad: Nápoj se má prodávat v plechovkách tvaru válce. Objem válce musí být 350 cm³. Jaké rozměry dají minimální povrch (a tedy mnimální cenu materiálu)?

Řešení: Klasický válec je dán dvěma parametry, svou výškou h a poloměrem podstavy r. Toto budou naše proměnné, jako jednotky použijeme centimetry. Řekli nám také, jaká "nákladová funkce" má být optimalizována: Je to povrch. Příslušný vzorec říká, že

S(r,h) = 2πr ² + 2πrh.

Máme také omezení, podmínku, kterou musíme dodržet. Říká, že

V(r,h) = πr ²h = 350.

Tuto podmínku můžeme použít k eliminaci jedné proměnné, zde bude asi snažší si vyjádřit h z naší podmínky a dosadit do vzorce pro povrch.

Chceme minimalizovat tuto funkci na množině všech rozumných hodnot r, což je v tomto případě interval I = (0,∞).

Abychom našli globální minimum, porovnáme hodnoty v podezřelých bodech. Dva podezřelé body jsou krajní body I, tedy 0 a nekonečno, ale protože vlastně neleží v I, použijeme k nalezení hodnoty limitu. Další podezřelé body jsou kritické body funkce S. Najdeme derivaci.

V I nejsou body, kde by derivace neexistovala, takže jediný zbývající zdroj podezřelých bodů jsou nulové body derivace. Rovnice S ′ = 0 dává řešení

Coby kladné číslo to leží v I, takže je to podezřelý bod. Teď dosadíme do S, třetí odmocnina tam padne lépe, když napíšeme r² jako r³/r.

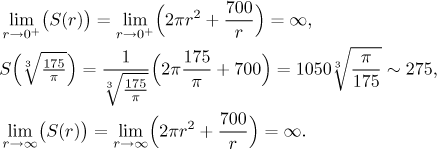
Vidíme, že minimální povrch se nabyde, když je r nulovým bodem derivace. Optimální rozměry plechovky tedy jsou

Upravili jsme vzorec pro h tak, aby se tam lépe dosazovalo r (coby třetí odmocnina). Výška je dvojnásobkem poloměru, takže optimální plechovka má stejnou výšku jako průměr a vypadá trochu "krychlovitě" (ze strany vypadá jako čtverec a vešla by se akorát do krychle). Mimochodem, příroda často potřebuje optimalizovat povrch. Pokud máme například určitý objem tekutiny, tak ona musí věnovat energii na udržení svého povrchu, tudíž v přírodě tekutina vždy zaujímá tvar s nejmenším povrchem (pokud nejsou další omezení). Proto také v beztížném stavu voda tvoří kapky tvaru koule. Kdyby nějaký kouzelník přinutil vodu dělat válečky, tak naše výpočty ukážaly, že by to byly válečky "krychlové", nikoliv podlouhlé.

Zpět k našemu příkladu. Jak to, že se nápoje neprodávají v takovýchto optimálních plechovkách? Důvod je, že je více věcí, na které je třeba brát ohled. Jedna důležitá je fakt, že se na spojích mezi základnami a stěnami utratí víc materiálu, takže je rozumné ty spoje dělat co nejmenší. Pokud plechovku protáhneme za stálého objemu, tak se její povrch zvětší, ale její poloměr se zmenší a tím ušetříme na těch drahých spojích. Další ohled se týká dopravy. Když dáme válce s velkým poloměrem do krabice, musíme tu krabici udělat velkou, protože mezi plechovkami se vyplýtvá spousta prostoru. Pokud jsou válce užší, pak se vyplýtvá méně místa. To souhlasí s naší každodenní zkušeností, určitě do sklenky nacpeme více materiálu, pokud použijeme jemný písek namísto velkých kamenů. Jsou tedy docela dobré důvody, proč dělat plechovky užší, asi jsou i další důvody (například že se možná lépe drží a lépe se z nich pije).

Další příklad
Zpět na Řešené příklady - Aplikace