Příklad: Najděte Taylorův polynom stupně 3 a stupně n se středem a = 0 pro funkci

f (x) = ln(1+2x).

Řešení: Taylorův polynom v a stupně 3 je dán vzorcem

Potřebujeme tedy spočítat první tři derivace a pak do nich dosadit a = 1. Vyplácí se dělat to systematicky, osobně to dělám takhle: Nejprve spočítám všechny derivace v jednom sloupci, pak udělám ta dosazení v druhém sloupci.

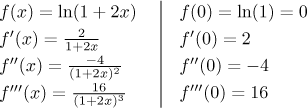
Teď toto a a dosadíme do obecného vzorce a dostaneme

Teď se podíváme na problém, jak uhodneme Taylorův polynom stupně n. Pro snadné případy je někdy možné to správně uhodnout z Taylorova polynomu stupně 3 nebo 4, ale zde by to mohlo být zrádné, ukážeme tedy postup, který je docela spolehlivý. Hlavní finta je nedívat se na čísla v pravém sloupci, ale zaměřit se na levý sloupec, kdy identifikujeme jednotlivé faktory, které se opakovaně objevují při výpočtu derivací. Co se děje, když derivujeme? Zopakujeme si výpočet těch derivací výše, abychom viděli, co se děje.

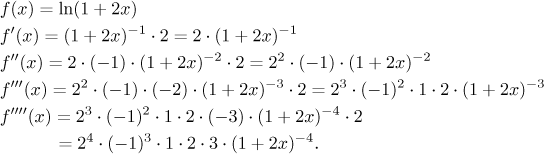
Už bychom měli vidět, jak to funguje. S každou derivací dostaneme navíc dvojku, přibude (−1) a pak rostoucí řetězec přirozených čísel, který vytváří faktoriál. Všimneme si také, že 2 dostaneme přesně tolikrát, kolikrát jsme derivovali, ale mocnina u (−1) a faktoriál jsou menší o jedno. Mocnina u (1+2x) souhlasí se řádem derivace (kromě toho mínusu). Jsme tedy připraveni formulovat obecnou hypotézu o k-té derivaci.

Ověříme, že to souhlasí s prvními třemi derivacemi, které jsme předtím spočítali, takže se zdá rozumné předpokládat, že to máme dobře, ale jen pro jistotu to dokážeme matematickou indukcí. Pro k = 1 to funguje, teď přejdeme od k ke k + 1.

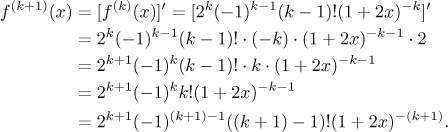
Toto dokazuje, že náš odhad k-té derivace je správný, můžeme tedy do něj dosadit 0 a pak to použít v obecném vzorci pro Taylorův polynom stupně n, nejprve použijeme sumační tvar, abychom zjednodušili výpočty. Připomeňme, že nultá derivace je daná jiným vzorcem, takže ji musíme při dosazování oddělit od ostatních.

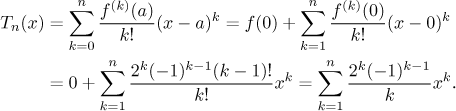
Ověřte, že první tři členy tohoto obecného vzorce souhlasí s naším T₃ výše.

Poznámka: Je snadnější způsob, jak najít T_n. Jedním z klasických výsledků, který se dá najít snad v každé učebnici zabývající se Taylorovými polynomy, je Taylorův polynom pro funkci ln(1+y).

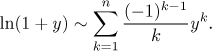
Když tam dosadíme y = 2x, dostaneme přesně ten výsledek, který jsme dostali přímým výpočtem.

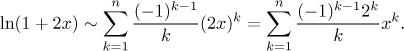
Poznámka: Toto je pěkný příklad, že při aproximaci pomocí Taylorových polynomů je třeba být opatrný. Pokud tuto aproximaci použijeme pro x = 1/4, pak bude dobrá, a její kvalita se jen zlepší se zvyšujícím se stupněm Taylorova polynomu. Dá se ale dokázat, že když do těch polynomů dosadíme x = 1, tak nebudou vůbec aproximovat ln(3), dokonce jejich hodnoty s rostoucím stupněm začnou silně oscilovat. Pro hlubší náhled do této problematiky viz Taylorovy řady v části Řady - Teorie - Řady funkcí.

Další příklad
Zpět na Řešené příklady - Aplikace