Implicitní funkce and implicitní derivování

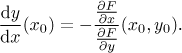
Začneme s trochou teorie, která zachází trochu dál, než jsme teď (alespoň oficiálně, jmenovitě potřebujeme použít funkce více proměnných), pak se podíváme na praktický přístup.

Uvažujme rovnici F(x,y) = c a bod (x₀,y₀), který splňuje tuto rovnici, tj, bod ležící na množině popsané touto rovnicí. S trochou štěstí existuje okolí tohoto bodu, na kterém je tato množina vlastně křivka, kterou lze popsat funkcí y = y(x). V sekci Implicitní funkce v části Funkce - Teorie máme Větu o implicitní funkci, kde je dostačující podmínka pro to, aby tomu tak bylo. Ukáže se, že tato podmínka je už dost silná i na to, aby zaručovala diferencovatelnost y(x) v daném bodě, věta nám dokonce řekne, jak tuto derivaci najít.

Věta (o implicitní funkci).
Uvažujme rovnici F(x,y) = c. Nechť bod (x₀,y₀) splňuje tuto rovnici. Jestliže

pak existuje okolí U bodu x₀ a funkce y = y(x) na tomto okolí taková, že y(x₀) = y₀ a F(x,y(x)) = c pro všechna x z U.

Tato funkce je navíc diferencovatelná v x₀ a

Použili jsme Leibnizovo značení, protože je z něj jasné, vzhledem ke které proměnné derivujeme. I když je to pravidlo pěkné, zřídkakdy jej použijeme doslovně; většinou opakujeme postup, kterým se dostane.

Důkaz tohoto pravidla je docela snadný. Vezmeme původní rovnici F(x,y) = c, předpokládáme, že y je vlastně funkce x, a zderivujeme obě strany. Pokud se rovnají původní výrazy, pak se také musí rovnat derivace. Když derivujeme nalevo, musíme použít řetízkové pravidlo (skládáme funkci F s funkcí y(x)), v tomto případě použijeme zobecnění řetízkového pravidla pro funkce více proměnných.

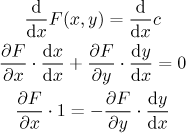
Z poslední rovnosti dostaneme vzorec ve větě. Trik s derivováním rovnice a pak vyjádřením derivace y se nazývá implicitní derivování a je to ten nejjednodušší způsob, jak získat derivaci implicitní funkce.

Příklad: V sekci Implicitní funkce v části Funkce - Teorie jsme dokázali, že rovnice y³ + 1 = xy definuje implicitní funkci y(x) na nějakém okolí bodu (2,1). Najděte tečnu k jejímu grafu v tomto bodě.

Řešení: Abychom dostali tečnu, potřebujeme bod - což máme - a její směrnici, jmenovitě potřebujeme y′ v x₀ = 2. K nalezení této derivace použijeme implicitní derivování. Zderivujeme obě strany dané rovnice, přitom budeme pamatovat na to, že y je vlastně funkce x. Uděláme to pomalu se všemi detaily, ať pořádně vysvětlíme, co se děje.

[(y(x))³ + 1]′ = [x⋅y(x)]′
3(y(x))²⋅[y(x)]′ = [x]′⋅y(x) + x⋅[y(x)]′
3(y(x))²⋅y′(x) = y(x) + x⋅y′(x)

Dostali jsme rovnici, ve které se vyskytuje y′(x), takže ji můžeme pro tuto derivaci vyřešit. Pak ale budeme potřebovat derivaci v jednom konkrétním bodě, takže možná bude snadnější rovnou dosadit.

3(y(2))²⋅y′(2) = y(2) + 2y′(2).

Kolik je y(2)? Naše implicitní funkce prochází bodem (2,1), proto y(2) = 1, tudíž

3⋅1²⋅y′(2) = 1 + 2y′(2).

Odtud dostaneme y′(2) = 1 a jsme připraveni napsat tu tečnu:

y = 1⋅(x − 2) + 1,     y = x − 1.

Poznámka: Zkušený student by ušetřil trochu psaní tím, že by nepsal to (x) vedle y v rovnici, je možné derivovat rovnici tak, jak byla napsána, a přitom myslet na to, že y je funkce x, a dostal stejný výsledek, například tento řádek:

3y²y′ = y + xy′.

Namísto dosazení x = 2 se dá tato rovnice vyřešit pro derivaci a dostaneme

Tento výraz je pak možné použít k nalezení derivace ve všech bodech z okolí, kde toto y(x) popisuje danou křivku (poznamenejme, že potřebujeme znát obě souřadnice, abychom mohli použít tento vzorec pro y′, protože obsahuje jak x, tak y = y(x)).

Pokud zderivujeme znovu rovnici, kterou jsme dostali, dostaneme druhou derivaci.

[3y²y′]′ = [y + xy′]′
[3y²]′y′ + 3y²[y′]′ = [y]′ + [x]′y′ + x[y′]′
6yy′y′ + 3y²y′′ = y′ + y′ + xy′′
6y(y′)² + 3y²y′′  = 2y′ + xy′′

Odtud máme

Podobně najdeme derivace vyššího řádu.

Pro přehled a příklad implicitního derivování viz Implicitní derivování v Přehledu metod.

Derivace parametrické funkce
Zpět na Teorie - Implicitní a parametrické funkce